Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{BH}{IH}=\dfrac{AB}{AI}\Rightarrow\dfrac{BH}{4}=\dfrac{AB}{5}\) \(\Rightarrow AB=\dfrac{5BH}{4}\)
Áp dụng định lý Pitago cho tam giác ABH:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow\left(\dfrac{5BH}{4}\right)^2=BH^2+9^2\)
\(\Rightarrow BH^2=144\Rightarrow BH=12\)
\(\Rightarrow BC=24\)

a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(Gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{AB}{3}=\dfrac{BC}{5}\)
Ta có: AD+CD=AC(D nằm giữa A và C)
nên AC=3+5=8(cm)
Đặt \(\dfrac{AB}{3}=\dfrac{BC}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=3k\\BC=5k\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\left(3k\right)^2+8^2=\left(5k\right)^2\)
\(\Leftrightarrow9k^2+64=25k^2\)
\(\Leftrightarrow16k^2=64\)
\(\Leftrightarrow k^2=4\)
hay k=2
Suy ra: \(\left\{{}\begin{matrix}AB=3\cdot k=3\cdot2=6\left(cm\right)\\BC=5\cdot k=5\cdot2=10\left(cm\right)\end{matrix}\right.\)
Vậy: AB=6cm; BC=10cm

- Trường hợp tam giác vuông:
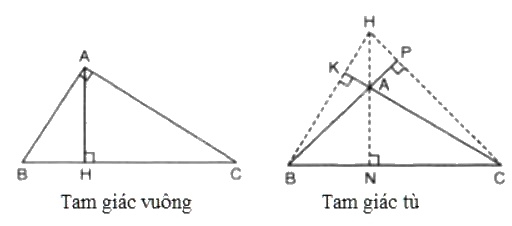
+) Xét tam giác ABC vuông tại A thì BA ⊥ CA hay A là giao điểm của hai đường vuông góc trong tam giác
⇒⇒ A trực tâm của tam giác.
Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.
+) Trường hợp tam giác tù:
Từ B kẻ đường thẳng BK vuông góc với CA.
Ta có: KA, KC lần lượt là hình chiếu của BA, BC.
Vì BC > BA nên KC > KA hay K phải nằm ngoài đoạn thẳng AC. Do đó ta có đường cao BK như hình vẽ.
Tương tự với đường cao CP.
Gọi H là giao điểm của BK và CP
⇒⇒ H chính là trực tâm của tam giác.
Ta thấy H ở bên ngoài tam giác.
Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác đó.
Cách 2:
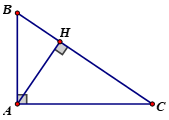
+ Xét ΔABC vuông tại A
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
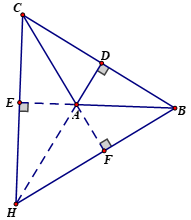
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B, khi đó
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
https://www.google.com/search?sxsrf=ACYBGNShkLL-JlrB5LGT8WMfh0jTHv-mgw:1581944122307&q=-Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+c%C3%A2n+t%E1%BA%A1i+A.+G%E1%BB%8Di+I,+K+theo+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB,+AC.+G%E1%BB%8Di+H,D+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+I,A+tr%C3%AAn+BK,+M+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+A+tr%C3%AAn+HI.+O+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BM+v%C3%A0+AC+,P+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB+v%C3%A0+DM+a)+C/m+tam+gi%C3%A1c+DAK+%3D+tam+gi%C3%A1c+HBI+b)+T%C3%ADnh+s%E1%BB%91+g%C3%B3c+ADC+c)C/m+OP+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC&tbm=isch&source=univ&sa=X&ved=2ahUKEwi7rNuL0djnAhUKzTgGHYr8DnMQsAR6BAgDEAE&biw=1137&bih=692
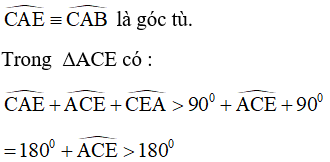
Bít chết liền
các bạn giải hộ mình phần c thôi nhé!