Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta MBD\)và \(\Delta MAC\)
có: \(\widehat{MAC}=\widehat{MBD}\)( cùng chắn cung MC)
\(\widehat{BMD}=\widehat{AMC}\)( cung AB=cung AC vì AB=AC)
=> \(\Delta MBD\)~ \(\Delta MAC\)
b) Từ câu a)_
=> \(\frac{MB}{MA}=\frac{BD}{AC}\)(1)
\(\frac{MC}{MA}=\frac{MD}{MB}\)(2)
Dễ dàng chứng minh đc:
\(\Delta BDM~\Delta ADC\)
=> \(\frac{MD}{MB}=\frac{DC}{AC}\)(3)
Từ (1), (2), (3)
=> \(\frac{MB}{MA}+\frac{MC}{MA}=\frac{BD}{AC}+\frac{CD}{AC}=\frac{BC}{AC}\)\(=\frac{BC}{AB}\)
c) Lấy điểm E thuộc đoạn

Do tính đối xứng, không mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow BH=CH=AH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(BH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(BH^2+MH^2\right)}=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)

Do tính đối xứng, ko mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow AH\) đồng thời là trung tuyến
\(\Rightarrow AH=\dfrac{1}{2}BC\Rightarrow AH=BH=CH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-HM\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(AH-MH\right)^2+\left(AH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)

a,xét tam giác DMB và DCA có:
góc BDM=ADC
góc BMD=ACD(góc nt cug chắn cug AB)
=>2 tam giác này đồng dạng vs nhau
a, xé tam giác MBD cà MAC có:
góc MBD=MAC( góc nt cug chắn cung MC)
góc BMA=AMC(chắn 2 cug bằng nhau)
=>2 tam giác này đồng dạng vs nhau

Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK
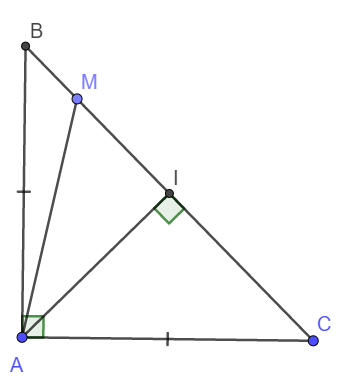
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.
\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)
Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )
Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)
\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)
\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)
\(=2AM^2\)
Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)

Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: \(BC=a\sqrt{2};\text{ }IB=IC=\frac{IA}{2}=\frac{a}{\sqrt{2}}\)
+Ta có: \(MB^2+MC^2=\left(\frac{a}{\sqrt{2}}-IM\right)^2+\left(\frac{a}{\sqrt{2}}+IM\right)^2=a^2+2IM^2\text{ (1)}\)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
\(\Rightarrow AM^2=AI^2+IM^2=\left(\frac{a}{\sqrt{2}}\right)^2+IM^2=\frac{a^2}{2}+IM^2\)
\(\Rightarrow2AM^2=a^2+2IM^2\text{ (2)}\)
Từ (1) và (2) suy ra \(MB^2+MC^2=2MA^2\)
Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: BC=a√2; IB=IC=IA2 =a√2
+Ta có: MB2+MC2=(a√2 −IM)2+(a√2 +IM)2=a2+2IM2 (1)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
⇒AM2=AI2+IM2=(a√2 )2+IM2=a22 +IM2
⇒2AM2=a2+2IM2 (2)
Từ (1) và (2) suy ra MB2+MC2=2MA2

Từ MM kẻ MEME vuông góc với ABAB, MFMF vuông góc với ACAC.
Ta có ΔEBMΔEBM vuông cân tại EE, ΔFMCΔFMC vuông cân tại FF và AEMFAEMF là hình chữ nhật.
Áp dụng định lý PytagoPytago vào các tam giác EBM,FMC,AEFEBM,FMC,AEF, ta có:
BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2) (1)
Mà AM2=EF2=ME2+MF2AM2=EF2=ME2+MF2 (2)
Từ (1),(2)(1),(2) ta có dpcmdpcm

Từ MM kẻ ME vuông góc với ABAB, MFMF vuông góc với ACAC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM,FMC,AEF, ta có:
BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2) (1)
Mà AM2=EF2=ME2+MF2AM2=EF2=ME2+MF2 (2)
Từ (1),(2)(1),(2) ta có dpcm