Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 6:
a: Xét tứ giác AKDH có
\(\widehat{AKD}=\widehat{AHD}=\widehat{KAH}=90^0\)
Do đó: AKDH là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=BC/2=2,5(cm)
a. Tứ giác AKDH là hình chữ nhật , vì có góc \(DKA=KAH=DHA=90^o\)
b, áp dụng đl pytago vào tam giác vuông ABC có :
\(BC^2=AB^2+AC^2\Leftrightarrow BC=\sqrt{4^2+3^2}=5cm\)
vì AD là trung tuyến tam giác vuông ABC nên :
\(AD=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5cm\)
c,vì AKDH là hình chữ nhật nên : DH//KA
mà D là trung điểm BC
=>H là trung điểm AC
<=>AH=\(\dfrac{1}{2}AC=\dfrac{1}{2}.3=1,5cm\)
vì AH = 1,5 cm nên => KD cũng = 1,5cm (AKDH là hình chữ nhật)
\(S_{ABD}=\dfrac{1}{2}.AB.KD=\dfrac{1}{2}.4.1,5=3cm^2\)

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: DA=DH
DH<DC
=>DA<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B

a/ Tứ giác AKDH có:
^BAC = ^AKD = ^AHD = 90° (GT).
=>AKDH là hình chữ nhật
b/ Áp dụng định lí Pythagoras vào ∆ABC vuông tại A có:
BC^2=AB^2+AC^2.
=>BC^2=9+16=25
=> BC = 5 (cm)
Xét ∆ABC vuông tại A có AD là đường trung tuyến.
=>AD = 1/2BC=2,5 (cm)
b/ Có:
DK vuông góc vs AB.
AB vuông góc vs AC.
=> DK // AC.
Xét ∆ABC có:
DK // AC, K thuộc AB.
D là trung điểm BC.
=> K là trung điểm AB (đ/l)
=> KD là đường trung bình ∆ABC
=> KD = 1/2AC=1,5(cm)
Có
S_(∆ABC)=1/2.KD.AB
=1/2.4.1,5
=2.1,5=3 (cm²)

xét tam giác ABC vuông tại A có \(BC^2=AB^2+AC^2\left(pytagor\right)\)
\(\Rightarrow BC=10\left(cm\right)\)
xét tam giác ABC ta có AD là đường phân giác => \(\frac{BD}{AB}=\frac{DC}{AC}=\frac{BC}{AB+AC}=\frac{5}{7}\)
=> BD= 30/7 (cm) ; DC= 40/7 (cm)
b/ có DH vuông góc AB ; AC vuông góc AB (tam giác vuông)
=> DH//AC => \(\frac{DH}{AC}=\frac{BD}{BC}=\frac{BH}{AB}\)(hệ quả Thales) => \(DH=\frac{AC.BD}{BC}=\frac{24}{7}\left(cm\right)\)
ta có HAD=CAD (p/giác) ; HDA=CAD( 2 góc slt; DH//AC) => HAD=HDA => tam giác AHD cân tại H
mà tam giác AHD vuông tại H => tam giác AHD vuông cân tại H
=> \(AD^2=2DH^2\)=> \(AD=\frac{24\sqrt{2}}{7}\left(cm\right)\)
mình ko tính ra số thập phân. Bạn tự tính nhé. Chúc bn học tốt

Áp dụng Pitago ta có : BC = 10
Áp dụng tính chất của tia phân giác ta có : BD/DC = AB/AC = 3/4
=> BD/BC = 3/7 => BD = 30/7 cm, CD = 40/7 cm
HD // AC => HD / AC = BD / BC
=> HD = 30/70.8 = 24/7
Do góc HAD = 45 độ => T/g HAD vuông cân => AD^2 = 1152/49 => AD = \(\frac{24\sqrt{2}}{7}\)cm

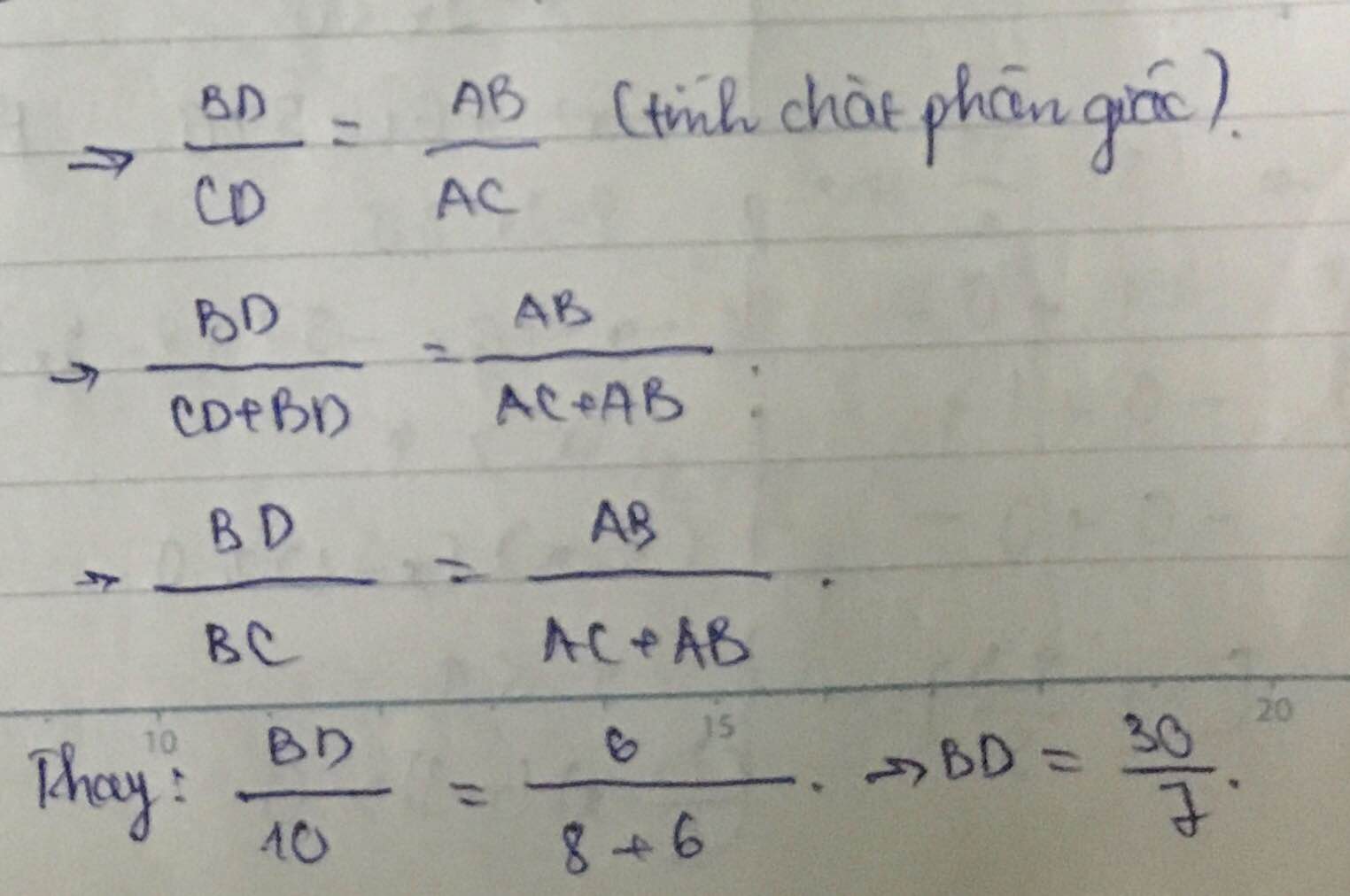
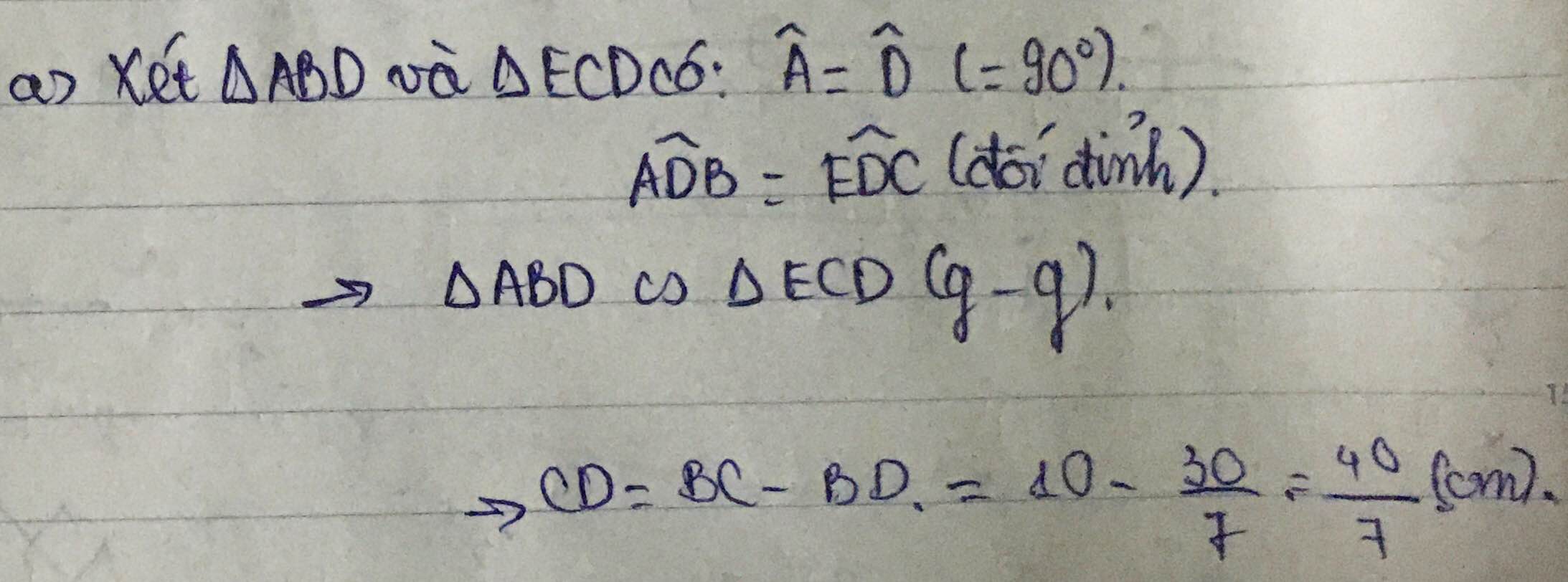
ai làm hộ mink cái Thanks
bạn lớp mấy ?