Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng định lí Pytago cho ∆ABC ta có:
AB2 + AC2 = BC2
=> AB2 + 82 = 102
=> AB2 = 100 - 64 = 36
=> AB = 6 cm
Vì AB = AD mà A nằm giữa B và D (cách vẽ) => BD = 2AB = 12cm
b, Xét ∆ABC và ∆ADC, ta có:
- AB = AD (gt)
- góc DAC = góc BAC = 90o
- CA là cạnh chung (gt)
=> ∆ABC = ∆ADC (c-g-c)
c, Xét ∆ECD và ∆EBF, ta có:
- góc FBE = góc DCE [so le trong]
- EB = EC (E là trung điểm BC)
- góc CED = góc BEF (đối đỉnh)
=> ∆ECD = ∆EBF (g-c-g)
=> DE = EF
d,
Vì ∆ECD = ∆EBF => CD = BF
Mà DB + BF > DF (bất đẳng thức tam giác)
\(\Rightarrow\frac{DB+BF}{2}>\frac{DF}{2}=DE\)
\(\Leftrightarrow\frac{DB+DC}{2}>DE\)

(Hình minh họa)
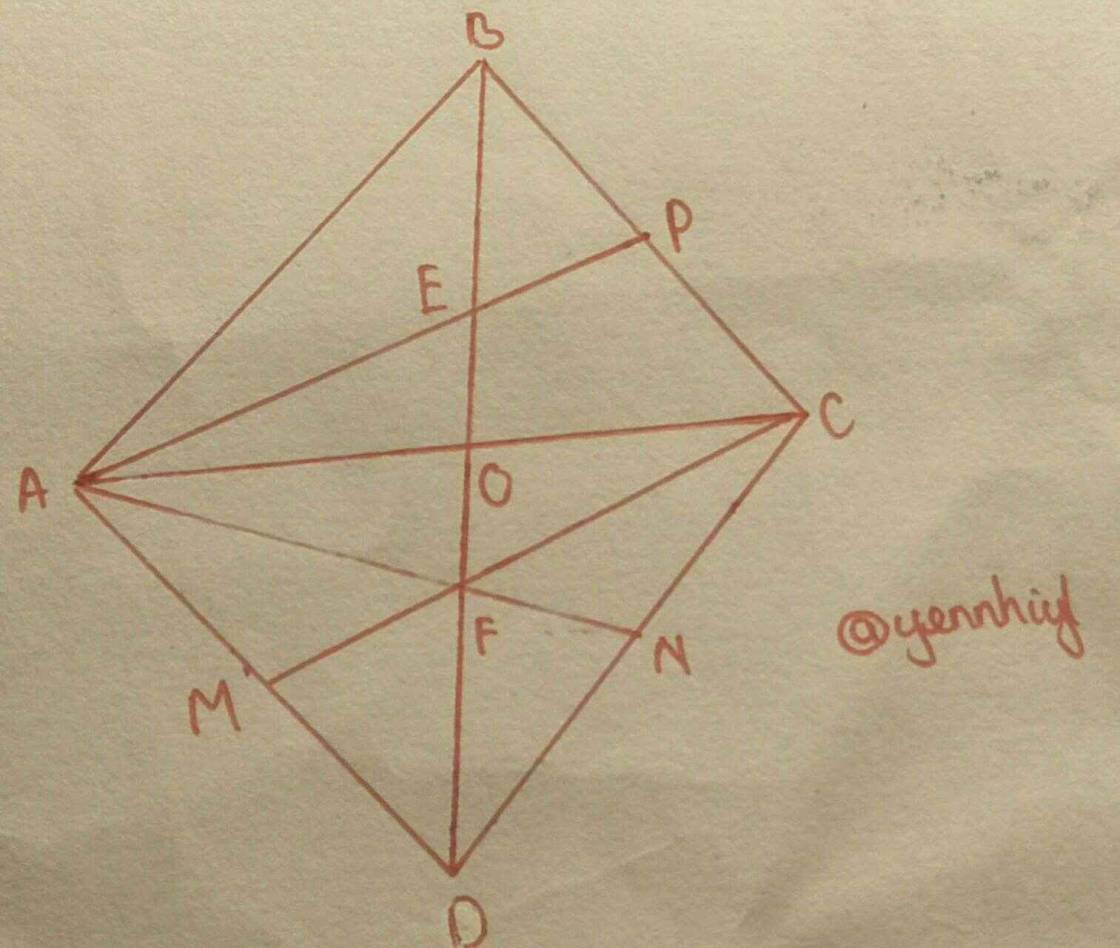
a)
Gọi O là giao điểm của AC và BD
Xét \(\Delta ABD\) và \(\Delta CDB\):
BD chung
\(\widehat{ABD}=\widehat{CDB}\)
\(\widehat{ADB}=\widehat{CBD}\)
\(\Rightarrow\Delta ABD=\Delta CBD\left(g.c.g\right)\)
\(\Rightarrow AB=CD\)
Xét \(\Delta AOB\) và \(\Delta COD\):
AB = CD
\(\widehat{OBA}=\widehat{ODC}\)
\(\widehat{OAB}=\widehat{OCD}\)
\(\Rightarrow\Delta AOB=\Delta COD\left(g.c.g\right)\)
\(\Rightarrow OA=OC;OB=OD\)
\(\Rightarrow O\) là trung điểm AC và BD
Xét \(\Delta ACD\):
MC và DO là hai đường trung tuyến của tam giác và giao nhau ở F
\(\Rightarrow F\) là trọng tâm \(\Delta ADC\)
Mà AN là đường trung tuyến \(\Delta ADC\)
\(\Rightarrow A,F,N\) thẳng hàng
b)
Vì P là trọng tâm \(\Delta ADC\)
\(\Rightarrow DF=\dfrac{2}{3}DO;OF=\dfrac{1}{3}DO\)
Vì O là giao điểm của hai đường trung tuyến BO và AP của \(\Delta ABC\)
\(\Rightarrow O\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow BE=\dfrac{2}{3}BO;EO=\dfrac{1}{3}BO\)
Mà O là trung điểm BD
\(\Rightarrow BO=DO\)
\(\Rightarrow BE=DF=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow FO=EO=\dfrac{1}{3}BO=\dfrac{1}{3}DO\Rightarrow EO+FO=FE=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow BE=FE=FD\).

a. Do AB//CD nên góc ABD = BDC, ADB = CBD. Suy ra \(\Delta ABD=\Delta CDB\left(g-c-g\right)\Rightarrow AB=CD,AD=BC\)
b. Dễ thấy \(\Delta AOB=\Delta COD\left(g-c-g\right)\Rightarrow OA=OC,OB=OD\)
c. Xét tam giác ABC có AM và BO là các đường trung tuyến nên E là trọng tâm, vậy OB = 2EO.
Tương tự DF=2FO. Mà OD = OB. Vậy BE = EF = DF.