Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(BM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
Tam giác ABM có MD là p/giác
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{AM}{BM}=\dfrac{6}{5}\)
b) Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{MC}{AM}=\dfrac{EC}{AE}\)
Mà: MC = BM (GT)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{EC}{AE}\)
c) Có: \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\left(cmt\right)\) (1)
Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{MC}\)
Mà: BM = MC (GT)
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{BM}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\)
=> DE // BC
a) Ta có: M là trung điểm của BC(gt)
nên \(MB=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔAMB có MD là đường phân giác ứng với cạnh AB(Gt)
nên \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{BD}=\dfrac{6}{5}\)

a: AD/BD=AM/MB=6/5
b: AE/EC=AM/MC=6/5
=>AD/BD=AE/EC
=>DE//BC
c: Để DE là đường trung bình thì D là trung điểm của AB, E là trung điểm của AC
Xét ΔAMB có
MD vừa la trung tuyến, vừa là phân giác
=>ΔMAB cân tại M
=>MA=MB=MC=1/2BC
=>ΔABC vuông tại A

a: AD/BD=AM/MB=6/5
b: AE/EC=AM/MC=6/5
=>AD/BD=AE/EC
=>DE//BC
c: Để DE là đường trung bình thì D là trung điểm của AB, E là trung điểm của AC
Xét ΔAMB có
MD vừa la trung tuyến, vừa là phân giác
=>ΔMAB cân tại M
=>MA=MB=MC=1/2BC
=>ΔABC vuông tại A

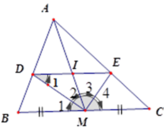
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE
Đặt DI = MI = x, ta có D I B M = A I A M (cmt) nên x 15 = 10 − x 10
Từ đó x = 6 suy ra DE = 12cm
Đáp án: D

a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔMAC ó ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>ED//BC
b: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=5/3
=>AD/AB=5/8
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/6=5/8
=>DE=3,75cm

Tam giác ABC có chu vi bằng 74cm, AC là cạnh lớn nhất. Đường phân giác của góc A chia cạnh BC thành hai đoạn tỉ lệ với 2:3; đường phân giác của góc C chia cạnh AB thành hai đoạn tỉ lệ với 4:5. Tính độ dài các cạnh của tam giác ABC.
AB + BC + AC = 74 (*)
Trong ∆ ABC phân giác AD → AB/AC = DB/DC = 2/3 (AC > AB)
→ AB = 2/3 . AC (1) , tương tự với phân giác CE ta suy ra
BC = 4/5 . AC (2) . Thế tất cả vào (*) ta được:
2/3 . AC + 4/5 . AC + AC = 74 → 37AC/15 = 74 → AC = 30cm
thế vào (1) và (2) ta được AB = 10cm, BC = 24cm