Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết ta có PN là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{PN}=\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{BM}\)
Do đó:
\(\overrightarrow{BM}+\overrightarrow{NC}=\overrightarrow{PN}+\overrightarrow{NC}=\overrightarrow{PC}\)
b.
Theo tính chất trọng tâm: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\left(\overrightarrow{AG}+\overrightarrow{GM}\right)\)
\(\Rightarrow\dfrac{1}{3}\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{GM}\Rightarrow2\overrightarrow{MG}=-\overrightarrow{AG}=\overrightarrow{GA}\)
\(\Rightarrow\overrightarrow{GB}+\overrightarrow{GC}+2\overrightarrow{MG}=\overrightarrow{GC}+\overrightarrow{GB}+\overrightarrow{GA}=\overrightarrow{0}\)

Ta có \(\overrightarrow{IB}=\overrightarrow{BA}\Rightarrow\hept{\begin{cases}I\in AB\\\overrightarrow{AI}=2\overrightarrow{AB}\end{cases}}\). Tương tự \(\hept{\begin{cases}J\in\left[AC\right]\\\overrightarrow{AJ}=\frac{AJ}{AC}\overrightarrow{AC}=\frac{2}{5}\overrightarrow{AC}\end{cases}}\)
Do đó \(\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\frac{2}{5}\overrightarrow{AC}-2\overrightarrow{AB}\)(đpcm).
giải giúp t câu này nha : tính vecto IG theo vecto AB và vecto AC (các b vẽ hình ra hộ t nhé)

a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)

\(\overrightarrow{GE}=\dfrac{1}{3}\overrightarrow{AG}=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
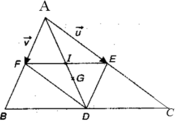
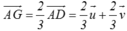
vecto MG=1/3vecto MA
=-1/3*vecto AM
=-1/3*1/2(vecto AB+vecto AC)
=-1/6*vecto AB-1/6*vecto AC