Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta gọi diện tích = S
theo đề ra ta có S(ADE) = EH x 1,8 : 2 =2,4 cm2
từ đó suy ra EH = 2,4 x 2: 1,8 <=> 2,6 cm ( lưu ý <=> nghĩa là tương đương kết quả chứ ko thể đúng kết quả)
ta lại có AE = \(\frac{2}{3}\) AC suy ra S(AEB) = \(\frac{2}{3}\)S(ABC)
vì diện tích hai hình này có cùng độ cao hạ từ B xuống AC và đáy AE = \(\frac{2}{3}\)đáyAC ( dựa vào tích chất cạnh nào cũng làm được đáy của hình tam giác)
suy ra S (AEB) = 10 x\(\frac{2}{3}\)<=> 6,6 cm2( dấu <=> biểu thị kết quả tương đương chứ ko đúng kết quả đc)
mà S(AEB) = EH x AB suy ra EH x AB = 6,6 cm2
suy ra 2,6 x AB = 6,6 cm2
suy ra AB = 6,6 : 2,6 <=> 2,6 cm (dấu <=> biểu thị kết quả tương đương chứ ko đúng kết quả)
vậy AB <=> 2,6 cm
(lưu ý lần sau ra đề nhớ chọn đề đẹp tí chọn đề lẻ quá)
bạn ra đề lẻ quá nên chia nó ko ra kết quả đúng chỉ có kết quả tương đương thui

a) ta thấy tỉ số diện tích tam giác ANB/ABC=1/3
tỉ số diện tích tam giác AMN/ANB=1/3 ( có chung chiều cao hạ từ N)
diện tích tam giác AMN là:
b) C với D như hình vẽ
ta thấy diện tích hai tam giác NDE bằng diện tích tam giác NDC ( có chung chiều cao và đáy )
từ đó suy ra:
vậy AND/NDE=1/2

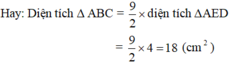
 Đẹp Không các bạn
Đẹp Không các bạn
Lấy M là trung điểm của DB
=>AD=DM=MB=1/3AB
Xét ΔAMC có AD/AM=AE/AC
nên ΔADE đồng dạng với ΔAMC
=>\(\dfrac{S_{ADE}}{S_{AMC}}=\left(\dfrac{AE}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMC}=40\left(cm^2\right)\)
AM=2/3AB
=>\(S_{ABC}=\dfrac{3}{2}\cdot S_{AMC}=60\left(cm^2\right)\)