Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MA+MC= MA-MB
<=> 2 MI=BA
=> MI=BA/2
=> I thuộc đường tròn I bán kính AB/2
nãy mk quên giải thik:
a, gọi I la trung điểm của AC=> MA+MC=2MI
hok tốt

a: Gọi M là trung điểm của AB
Xét ΔABC có
G là trọng tâm
M là trung điểm của AB
Do đó: CG=2/3CM
=>CG=2GM
=>\(\overrightarrow{CG}=2\overrightarrow{GM}\)
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)
\(=2\overrightarrow{GM}+\overrightarrow{GC}\)
\(=\overrightarrow{CG}+\overrightarrow{GC}=\overrightarrow{0}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
\(=3\cdot\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3\cdot\overrightarrow{MG}\)

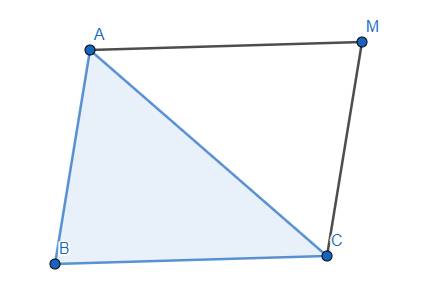
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.

\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)⇒ O là trọng tâm tam giác ABC
\(\overrightarrow{K\text{A}}+2\overrightarrow{KB}=\overrightarrow{CB}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KB}+\overrightarrow{BC}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KC}=\overrightarrow{0}\)
⇒ K là trọng tâm tam giác ABC
Câu cuối chịu :))

Xét ΔABC có G là trọng tâm
nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\dfrac{1}{3}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{3}\left(\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right)\)
\(=\dfrac{1}{3}\left(3\cdot\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=\dfrac{1}{3}\cdot3\cdot\overrightarrow{MG}=\overrightarrow{MG}\)
Bằng vec tơ gì bạn ơi ?