Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
Hình bình hành AEDF có AD là phân giác của góc FAE
nên AEDF là hình thoi
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{CD}{DB}=\dfrac{AC}{AB}\left(1\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{CD}{DB}=\dfrac{CE}{EA}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AC}{AB}=\dfrac{EC}{EA}\)
=>\(AC\cdot AE=AB\cdot EC\)

Do DE song song BC
=> Theo định lý Talet, DA/DB = EA/EC
Mà DA/DB= EC/EA
=> EC=EA
=> E là trung điểm AC
=> DE là đường trung bình của tam giác ABC
=> D cũng là trung điểm AB

Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^
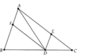

Hình tự vẽ nha bạn
Vì AD là đường phân giác của góc A
=> \(\widehat{BAD}=\widehat{DAE}\)
Vì AB//ED =>\(\widehat{BAD}=\widehat{EDA}\)(2 góc so le trong)
Mà góc BAD=góc DAE=> \(\widehat{DAE}=\widehat{EDA}\)
=> tam giác EAD cân tại E
=>EA=ED
Ta có: AB//ED cắt FE//BC => BF=ED(theo tính chất đoạn chắn)
Mà EA=ED=> AE=BF(=ED)

zì \(\hept{\begin{cases}MD//AE\\ME//AD\end{cases}}\)
=> tứ giác ADME là hbh
=>\(\hept{\begin{cases}AD=ME\\AE=MD\end{cases}}\)
=>\(\frac{AD}{AB}=\frac{ME}{AB}\)
mà ME//AB
=>\(\frac{ME}{AB}=\frac{CE}{AC}=>\frac{AD}{AB}=\frac{CE}{AC}\)
=>\(\frac{AD}{AB}+\frac{AE}{AC}=\frac{CE}{AC}+\frac{AE}{AC}=\frac{CE+AE}{AC}=\frac{AC}{AC}=1\left(dpcm\right)\)


Theo đề bài, AD là tia phân giác của \(\widehat {BAC}\), áp dụng tính chất đường phân giác vào tam giác ABC, ta có: \(\dfrac{{AC}}{{AB}} = \dfrac{{DC}}{{DB}}\) (1)
Đường thẳng qua D song song với AB cắt AC tại E hay DE // AB, áp dụng định lí Thalès vào tam giác ABC, ta có: \(\dfrac{{DC}}{{DB}} = \dfrac{{EC}}{{E{\rm{A}}}}\) (2)
Từ (1) và (2) suy ra \(\dfrac{{AC}}{{AB}} = \dfrac{{EC}}{{E{\rm{A}}}}\) (đpcm).