Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

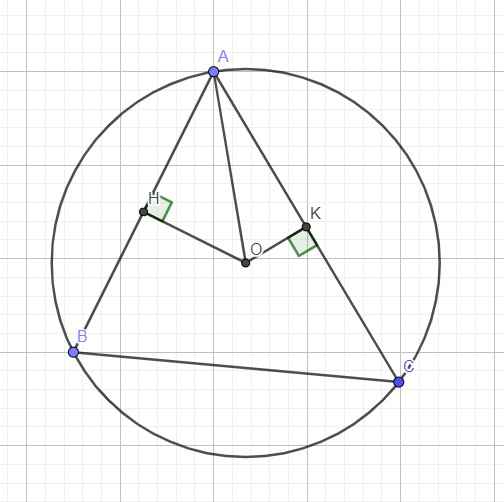
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) \(\Rightarrow OH=2\sqrt{2}\)
Áp dụng định lý Pitago cho tam giác OAH:
\(AH=\sqrt{OA^2-OH^2}=\sqrt{3^2-\left(2\sqrt{2}\right)^2}=1\)
\(\Rightarrow AB=2AH=2\left(cm\right)\)
Gọi K là trung điểm AC \(\Rightarrow OK\perp AC\Rightarrow OK=\dfrac{\sqrt{11}}{2}\)
Áp dụng định lý Pitago cho tam giác AOK:
\(AK=\sqrt{OA^2-OK^2}=\sqrt{3^2-\left(\dfrac{\sqrt{11}}{2}\right)^2}=2,5\left(cm\right)\)
\(\Rightarrow AC=2AK=5\left(cm\right)\)

Lời giải:
Kẻ $OM, ON$ lần lượt vuông góc với $AB, AC$
Vì $OAB$ là tam giác cân tại $O$ ($OA=OB=R=3$) nên đường cao $OM$ đồng thời là đường trung tuyến
$\Rightarrow M$ là trung điểm $AB$
Áp dụng định lý Pitago:
$MB=\sqrt{OB^2-OM^2}=\sqrt{3^2-(2\sqrt{2})^2}=1$
$\Rightarrow AB=2MB=2$ (cm)
Tương tự:
$N$ là trung điểm $AC$
$NC=\sqrt{OC^2-ON^2}=\sqrt{3^2-(\frac{\sqrt{11}}{2})^2}=2,5$ (cm)
$AC=2NC=2.2,5=5$ (cm)

Đặt AB = x ; AC = y ( ĐK x ; y > 0 )
BC = 2R = 2.5 = 10
Theo py ta go => x^2 + y^2 = BC^2 = 100
r = \(\frac{AB+AC-BC}{2}=\frac{x+y-10}{2}=3\Leftrightarrow x+y=16\) (2)
Từ (1) v/s (2) => x^2 + y^2 = 100
và x + y = 16