Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi G là trọng tâm tam giác
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{OG}=\overrightarrow{0}\)
\(\Leftrightarrow O\equiv G\)
\(\Rightarrow O\) là trọng tâm tam giác ABC
\(\Rightarrow\Delta ABC\) đều
Gọi độ dài các cạnh tam giác là a
\(\overrightarrow{BN}.\overrightarrow{AM}=\dfrac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=-\dfrac{1}{4}a^2-\dfrac{1}{8}a^2-\dfrac{1}{8}a^2+\dfrac{1}{2}a^2=0\)
Mặt khác \(\overrightarrow{BN}.\overrightarrow{AM}=BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)\)
\(\Rightarrow BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow\left(\overrightarrow{AM};\overrightarrow{BN}\right)=90^o\)
\(BD=\dfrac{AB}{cos45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{BQ}.\overrightarrow{BP}=\dfrac{1}{4}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{4}BA.BC.cos90^o+\dfrac{1}{4}BA.BD.cos45^o+\dfrac{1}{4}BD.BC.cos45^o+\dfrac{1}{4}BD^2\)
\(=\dfrac{1}{4}a^2+\dfrac{1}{4}a^2+\dfrac{1}{2}a^2=a^2\)

\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=a\) (a>0 mới đúng, độ dài ko thể nhỏ hơn 0)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=a\)
\(\Leftrightarrow3\left|\overrightarrow{MG}\right|=a\) (do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\))
\(\Leftrightarrow MG=\dfrac{a}{3}\)
\(\Rightarrow\) Tập hợp M là đường tròn tâm G bán kính \(\dfrac{a}{3}\)
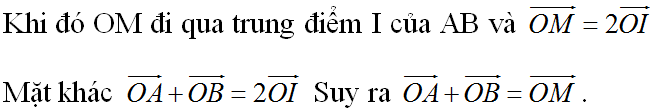

Gọi I là trung điểm của AC \(\Rightarrow IC=\frac{AC}{2}=2\) và \(\overrightarrow{OA}+\overrightarrow{OC}=2\overrightarrow{OI}\)
\(OI\perp AC\Rightarrow\Delta OIC\) vuông tại I, áp dụng Pytago:
\(OI=\sqrt{OC^2-IC^2}=\sqrt{5}\)
Ta có:
\(\overrightarrow{OM}=2\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{BM}=2\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{OB}-\overrightarrow{OA}+2\left(\overrightarrow{OA}+\overrightarrow{OC}\right)\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+4\overrightarrow{OI}\) \(\Leftrightarrow\overrightarrow{BM}=4\overrightarrow{OI}\)
\(\Rightarrow\left|\overrightarrow{BM}\right|=\left|4\overrightarrow{OI}\right|=4OI=4\sqrt{5}\)