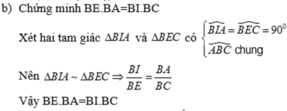Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
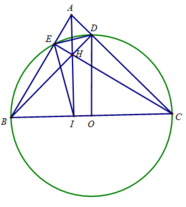
Gọi O là trung điểm của AB
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD vuông góc AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE vuông góc BC tại E
Xét tứ giác CDHE có
góc CDH+góc CEH=180 độ
=>CDHE nội tiếp
b: Xét ΔCAB có
AE,BD là đường cao
AE cắt BD tại H
=>H là trực tâm
=>CH vuông góc AB tại K
c: Xét ΔAKH vuông tại K và ΔAEB vuông tại E có
góc KAH chung
Do đó: ΔAKH đồng dạng với ΔAEB
=>AK/AE=AH/AB
=>AH*AE=AK*AB
Xét ΔBKH vuông tại K và ΔBDA vuông tại D có
góc KBH chung
Do đó: ΔBKH đồng dạng với ΔBDA
=>BK/BD=BH/BA
=>BK*BA=BH*BD
AH*AE+BH*BD
=AK*AB+BK*BA
=BA^2
a) ....................... =) C, D, H, E cùng thuộc 1 đường tròn.
b) ....................... =) CH ⊥ AB.
c) ....................... =) AH.AE + BH.BD = AB2.

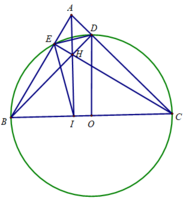
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC

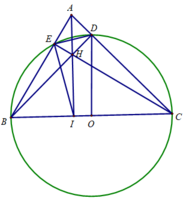
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256