Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
qua O x lay D sao cho D diểm doi sung cua a qua O x lay E sao cho E ldiểm em doi sung cua a qua O y doan DE cat O x dâuau thdiểmem B ở do, DE cat O y dâuau thi C ở dó
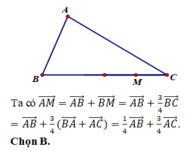
de dang Cdượcoc tam Giác ABC có chu vi nhnhấtat
- Tìm A’ đối xứng với A qua Oy , B’ đối xứng với A qua Ox
- Nối A’B’ cắt Ox tại B , cắt Oy tại C . Đó chính là hai điểm cần tìm
- Chứng minh B,C là hai điểm duy nhất cần tìm .
Thật vậy : Do A’ đối xứng với A qua Oy , cho nên CA=CA’ (1) . Mặt khác : B’ đối xứng với A qua Ox cho nên ta có BA=BB’ (2) .
Gọi P là chu vi tam giác ABC - do từ (1) và (2) - thì P=CA+CB+BA =CA’+CB+BB’=A’B’
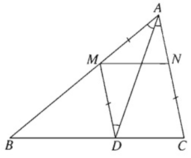
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó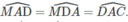 
. Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có
N
M
→
=
C
D
→
, nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ
D
C
→
.
Từ đó suy ra cách dựng:
- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.
- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ C D → . d cắt AB tại M.
- Dựng N sao cho N M → = C D → .
Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.
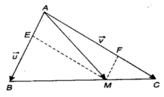
Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh
