Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

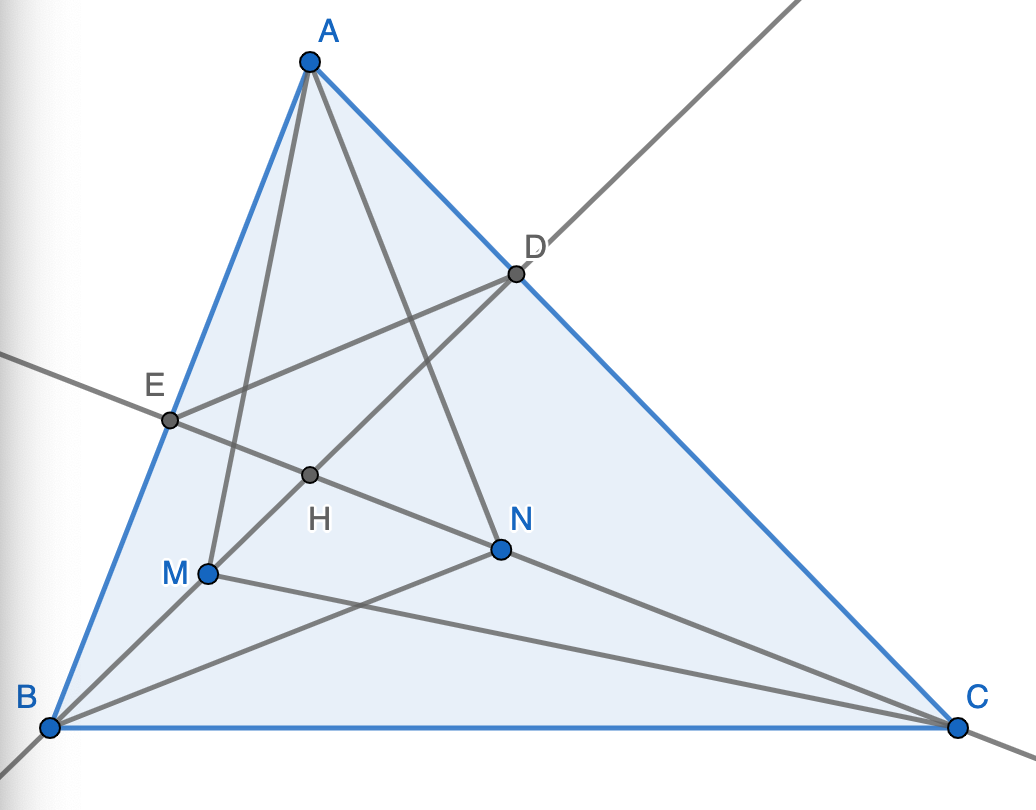
Tự vẽ hình nha bạn
Xét hai tam giác vuông : tam giác DAB và tam giác EAC có :
góc A là góc chung , góc EAC = góc ADB = 90 độ
=> tam giác DAB đồng dạng tam giác EAC
\(\Rightarrow\frac{AD}{AE}=\frac{AB}{AC}\Rightarrow AB\cdot AE=AD\cdot AC\)
Mặt khác, áp dụng hệ thức về cạnh trong tam giác vuông ABN có đường cao NE : \(AN^2=AE\cdot AB\)
Rồi áp dụng hệ thức đi nha

Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$

Tự vẽ hình nhá !
Theo hệ thức lượng trong tam giác vuông, ta có:
\(AB_1^2=AD.AC\)(1) ; \(AC_1^2=AE.AB\)(2)
Dễ thấy: \(\Delta\)ADB ~ \(\Delta\)AEC (g.g) \(\Rightarrow\frac{AD}{AE}=\frac{AB}{AC}\Rightarrow AD.AC=AE.AB\)(3)
Từ (1); (2) và (3) \(\Rightarrow AB_1^2=AC_1^2\Rightarrow AB_1=AC_1\). Suy ra \(\Delta\)AB1C1 cân tại A (đpcm).
Đố :Trang đố Nga dùng bốn chữ số 2 cùng với dấu phép tính và dấu ngoặc (nếu cần) viết dãy tính có kết quả lần lượt bằng 0,1,2,3,4

Xét ΔAB1C vuôg tại B1 có BD là đương cao
nên \(AD\cdot AC=AB_1^2\left(1\right)\)
Xét ΔAC1B vuông tại C1 có C1E là đường cao
nên \(AE\cdot AB=AC_1^2\left(2\right)\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
Do đó: ΔADB đồng dạng với ΔAEC
Suy ra: AD/AE=AB/AC
hay \(AD\cdot AC=AB\cdot AE\left(3\right)\)
Từ (1), (2) và (3) suy ra AB1=AC1(ĐPCM)