Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
=>AHBD là hình chữ nhật
b: \(AH=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{AHBD}=6\cdot8=48\left(cm^2\right)\)
c: Xét ΔABC có AM/AB=AI/AC
nênMI//BC
Xét ΔBAC có CN/CB=CI/CA
nên NI//AB và NI/AB=CN/CB=1/2
=>NI=HM
Xét tứ giác MINH có
MI//HN
MH=IN
Do đó: MINH là hình thang cân

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC
b, Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC=6\left(cm\right)\)
c, Vì MN//BC nên BMNC là hình thang

b: Xét tứ giác ABCE có
M là trung điểm của AC
M là trung điểm của BE
Do đó:ABCE là hình bình hành

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: \(MN=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

Ta có:
M là trung điểm AB
N là trung điểm AC
⇒ MN là đường trung bình cùa tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}BC\Rightarrow BC=2\cdot MN=2\cdot5=10\left(cm\right)\)
Xét tam giác ABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AC=\sqrt{10^2-6^2}=8\left(cm\right)\)

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
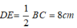
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
=
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu củ
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQMa A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc A
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
QM
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
tóm lị là ABGHMN là sai

Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Vậy \(MN=\dfrac{1}{2}BC=3\left(cm\right)\)
\(MN=\dfrac{BC}{2}=3\left(cm\right)\)