Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại I
b: Ta có: \(\widehat{AMO}=\widehat{ANO}=\widehat{AIO}\)
=>A,M,I,O,N cùng thuộc đường tròn đường kính AO
Gọi I là trung điểm của AO
=>A,M,I,O,N cùng thuộc (I)
Xét (O) có
AM,AN là các tiếp tuyến
Do đó: OA là phân giác của góc MON
=>\(\widehat{MOA}=\widehat{NOA}\)
Xét (I) có
\(\widehat{MOA}\) là góc nội tiếp chắn cung MA
\(\widehat{NOA}\) là góc nội tiếp chắn cung NA
\(\widehat{MOA}=\widehat{NOA}\)
Do đó: \(sđ\stackrel\frown{MA}=sđ\stackrel\frown{NA}\)
Xét (I) có
\(\widehat{MIA}\) là góc nội tiếp chắn cung MA
\(\widehat{NIA}\) là góc nội tiếp chắn cung NA
\(sđ\stackrel\frown{MA}=sđ\stackrel\frown{NA}\left(cmt\right)\)
Do đó: \(\widehat{MIA}=\widehat{NIA}\)
=>IA là phân giác của góc MIN

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
b: Ta có: H là trực tâm của ΔABC
nên AH⊥BC tại F
Xét ΔAEH vuông tại E và ΔAFB vuông tại F có
\(\widehat{EAH}\) chung
Do đó: ΔAEH\(\sim\)ΔAFB
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AH}{AB}\)
hay \(AE\cdot AB=AF\cdot AH\left(1\right)\)
Xét ΔADH vuông tại D và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔADH\(\sim\)ΔAFC
Suy ra: \(\dfrac{AD}{AF}=\dfrac{AH}{AC}\)
hay \(AD\cdot AC=AH\cdot AF\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AH\cdot AF=AD\cdot AC\)

a) Xét hai tam giác ABD và ACE có:
\(\widehat{A}\) chung
\(\widehat{ADB}=\widehat{AEC}=90^o\)
\(\Rightarrow\Delta ABD\sim\Delta ACE\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AC}=\frac{AD}{AE}\Rightarrow AD.AC=AE.AB\)
b) Xét tam giác ABC có BD và CE là hai đường cao nên H là trực tâm. Vậy thì AH vuông góc với BC tại K.
c) Ta thấy AMO; AKO; ANO là các tam giác vuông có chung cạnh huyền AO nên A, M, K, O, N cùng thuộc đường tròn đường kính AO.
Khi đó \(\widehat{AKN}=\widehat{AMN}\) (Hai góc nội tiếp cùng chắn cung AN)
Lại có AM = AN nên \(\widehat{AMN}=\widehat{ANM}\)
Suy ra \(\widehat{AKN}=\widehat{ANM}\)
d) Gọi J là giao điểm của MN với AO.
Xét tam giác vuông ANO, đường cao NJ, ta có:
\(AJ.AO=AN^2\) (Hệ thức lượng)
Lại có \(\Delta AHJ\sim\Delta AOK\left(g-g\right)\Rightarrow\frac{AH}{AO}=\frac{AJ}{AK}\)
\(\Rightarrow AJ.AO=AH.AK\)
\(\Rightarrow AN^2=AH.AK\)
\(\Rightarrow\Delta AHN\sim\Delta ANK\left(c-g-c\right)\Rightarrow\widehat{ANH}=\widehat{AKN}\)
Mà \(\widehat{AKN}=\widehat{ANM}\Rightarrow\widehat{ANH}=\widehat{ANM}\) hay M, N, H thẳng hàng.
Hoàng Thị Thu Huyền ơi ngộ nhận kìa. ý d đang chứng minh thẳng hàng mà bạn có 2 cái tam giác AHJ và AOK đồng dạng (g g) thì sao được ??

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC

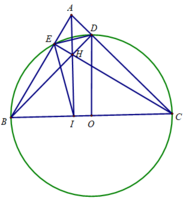
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)

đáng lẽ đề bài phải là AHcắt CB tại ii ms đúng bạn
a, AI vg vs BC vì tính chất 3 đường cao