Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em xem lại đề bài này nhé.
d. Do S, H cùng thuộc AH nên nếu S, H ,E thẳng hàng thì E phải thuộc AH. Cô có hình vẽ phản chứng:

a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).



d: \(SA^2=SB\cdot SC\)
\(SE^2=SB\cdot SC\)
=>SA=SE
Xét ΔOAS và ΔOES có
OA=OE
SA=SE
OS chung
Do đó: ΔOAS=ΔOES
=>\(\widehat{OAS}=\widehat{OES}\)
mà \(\widehat{OAS}=90^0\)
nên \(\widehat{OES}=90^0\)
=>E nằm trên đường tròn đường kính SO
mà S,A,O,D cùng thuộc đường tròn đường kính SO(cmt)
nên E nằm trên đường tròn (SAOD)

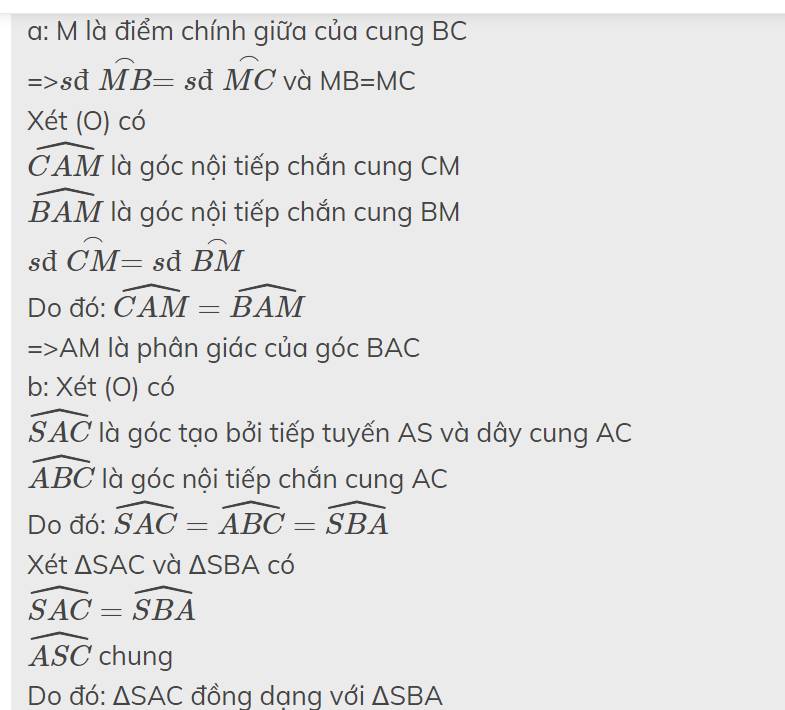
a: M là điểm chính giữa của cung BC
=>\(sđ\stackrel\frown{MB}=sđ\stackrel\frown{MC}\) và MB=MC
Xét (O) có
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
\(\widehat{BAM}\) là góc nội tiếp chắn cung BM
\(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BM}\)
Do đó: \(\widehat{CAM}=\widehat{BAM}\)
=>AM là phân giác của góc BAC
b: Xét (O) có
\(\widehat{SAC}\) là góc tạo bởi tiếp tuyến AS và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{SAC}=\widehat{ABC}=\widehat{SBA}\)
Xét ΔSAC và ΔSBA có
\(\widehat{SAC}=\widehat{SBA}\)
\(\widehat{ASC}\) chung
Do đó: ΔSAC đồng dạng với ΔSBA
=>\(\dfrac{SA}{SB}=\dfrac{SC}{SA}\)
=>\(SA^2=SB\cdot SC\)
c: Xét (O) có
góc CKA là góc có đỉnh ở trong đường tròn chắn cung AC và BM
=>\(\widehat{CKA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AC}+sđ\stackrel\frown{BM}\right)\)
=>\(\widehat{SKA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AC}+sđ\stackrel\frown{CM}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{AM}\)
mà \(\widehat{SAK}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AM}\)(góc tạo bởi tiếp tuyến SA và dây cung AM)
nên \(\widehat{SAK}=\widehat{SKA}\)
=>SA=SK
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OM là đường trung trực của BC
=>OM\(\perp\)BC tại D
Xét tứ giác SAOD có
\(\widehat{SAO}+\widehat{SDO}=90^0+90^0=180^0\)
nên SAOD là tứ giác nội tiếp
=>S,A,D,O cùng thuộc một đường tròn