Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình tự vẽ
ta có :
DE//BC (gt)
=>góc DIB = góc IBC( so le trong )
mà góc DBI= góc IBC (gt)
=>góc DIB= góc DBI
=>tam giác DIB là tam giác cân tại D
=>DI=DB
ta có : DE//BC(gt)
=>góc EIC = góc ICB (slt)
mà góc ECI = góc ICB (gt)
=>góc EIC = góc ECI
=>tam guacs EIC cân ở E
=>EI=EC
mà ED=IE+ID
=>ED=EC+BD

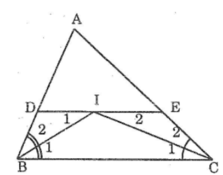
Ta có: DI // BC (giả thiết)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là tia phân giác góc ABC)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) => ∠I2 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc ACB) (5)
Từ (4) và (5) suy ra: ∠I2=∠C2. Suy ra ∠CEI cân tại E
Suy ra: CE = EI (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

ta có \(\widehat{DIB}=\widehat{IBC}\)(cặp góc so le trong)
mà \(\widehat{DBI}=\widehat{IBC}\)(BI là đường phân giác của \(\widehat{B}\)
=>\(\widehat{DIB}=\widehat{DBI}\)=>\(\Delta DIB\)cân tại D (hai góc ở đáy bằng nhau)
=> ID=BD(1)
Chứng minh tương tự ta có IE=CE(2)
Lấy (1) cộng (2) vế theo vế ta có ID+IE=BD+CE =>DE=BD+CE

Ta có hình vẽ:
Ta có: BI là pg góc B
=> góc DBI = góc IBC
Mà góc DIB = góc IBC (DE // BC)
=> góc DBI = góc DIB
=> tam giác BDI cân
=> BD = DI
Ta có: CI là phân giác góc C
=> góc ECI = góc ICB
Mà góc EIC = góc ICB (DE // BC)
=> góc ECI = góc EIC
=> tam giác CEI cân
=> CE = IE
Ta có: BD = DI; CE = IE
=> BD + CE = DI + IE
hay BD + CE = DE
hay DE = BD + CE
Ta có: DI // BC (gt)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là yia phân giác góc B)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) =>∠I1 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc C) (5)
Từ (4) và (5) suy ra: ∠C1=∠C2. Suy ra. ∠CEI cân tại E
Suy ra: CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

Bài 5:
a: Xét ΔDBI có \(\widehat{DIB}=\widehat{DBI}\)
nên ΔDBI cân tại D
hay DI=DB
b: Xét ΔCEI có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
c:Ta có: DI+IE=DE
nên DE=BD+CE

b)CIE = ICB (2 góc so le trong, DE // BC)
mà ICB = ICE (IC là tia phân giác của ECB)
=> CIE = ICE
=> Tam giác EIC cân tại I
=> EI = EC
BID = IBC (2 góc so le trong, DE // BC)
mà IBC = IBD (IB là tia phân giác của DBC)
=> BID = IBD
=> Tam giác DIB cân tại D
=> DI = DB
DE = DI + IE = DB + CE
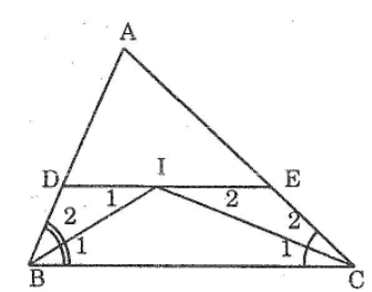
Ta có : góc DBI = góc IBC ( vì BI là tia phân giác của góc ABC )
góc DIB = góc IBC ( so le trong do DE // BC)
\(\Rightarrow\) góc DBI = góc DIB
\(\Rightarrow\Delta BDI\)cân tại D
\(\Rightarrow BD=DI\left(1\right)\)
Và ta lại có: góc ECI = góc ICB ( vì CI là tia phân giác của góc ACB)
góc EIC = góc ICB ( so le trong do DE// BC)
\(\Rightarrow\Delta CEI\) cân tại E
\(\Rightarrow CE=EI\left(2\right)\)
\(Mà:DI+EI=DE\left(I\in DE\right)\)
\(Hay:BD+CE=DE\left(từ1\&2\right)\)
\(\Rightarrowđpcm\)