Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nhé. EF cắt AH tại L.
Xét tam giác AIM vuông tại I(MI vuông góc AB) có HF//IM ( H là trực tâm nên HF vuông góc AB, từ vuông góc đến song song >> HF//IM) >> \(\frac{AF}{AI}=\frac{AH}{AM}\left(Talet\right)\)
CMTT >> \(\frac{AE}{AK}=\frac{AH}{AM}\left(Talet\right)\)>> \(\frac{AF}{AI}=\frac{AE}{AK}\). Theo Talet đảo có EF // IK.
Xét tam giác AIK có EF // IK >> AEF đồng dạng AIK ( bạn tự cm, quá dễ) >> góc AFE = góc AIK và góc AEF = góc AKI
Xét tam giác AFL và tam giác AID : chung góc A và AFL = AID (cmt) >> AFL đồng dạng AID >> ALF = ADI đồng vị >> ID // EL
CMTT thì LE // DK. Có E,L,F thẳng hàng nên theo tiên đề Euclid suy ra I,D,K thẳng hàng.
bạn ơi, AFL=AID đang cần chứng minh mà, AFL=AIK mới đúng. nếu AFL=AID=AIK thì I,D,K thẳng hàng rồi.

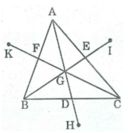
*) Tam giác ABC có ba đường trung tuyến AD, BE, CF cắt nhau tại G nên G là trọng tâm tam giác ABC.
* Ta có: GD = DH (tính chất đối xứng tâm)
⇒ GH = 2GD (l)
GA = 2GD (tính chất đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra: GA = GH
Suy ra điểm đối xứng với điểm A qua G là H.
* Ta có: GE = EI (tính chất đối xứng tâm)
⇒ GI = 2GE (3)
Lại có, GB = 2GE (tính chất đường trung tuyến của tam giác) (4)
Từ (3) và (4) suy ra: GB = GI
Suy ra điểm đối xứng với điểm B qua G là I.
+) Ta có: GF = FK (tính chất đối xứng tâm)
⇒ GK = 2GF (5)
GC = 2GF (tính chất đường trung tuyến của tam giác) (6)
Từ (5) và (6) suy ra: GC = GK
Suy ra điểm đối xứng với điểm C qua G là điểm K
Nối E với D.\(EK\cap BC=\left\{M\right\}\).
Xét tam giác DME và tam giác DMK ta có:
\(\left\{{}\begin{matrix}EM=KM\left(gt\right)\\\widehat{DME}=\widehat{DMK}\left(=90^o\right)\\DM:chung\end{matrix}\right.\)
Do đó \(\Delta DME=\Delta DMK\left(c.g.c\right)\)
\(\Rightarrow\widehat{MDE}=\widehat{MDK}\left(cgtu\right)\)(1)
mà \(\widehat{MDK}=\widehat{BDF}\left(d.d\right)\)
\(\Rightarrow\widehat{MDE}=\widehat{BDF}\)
Ta có:
\(\widehat{HDM}=\widehat{HDB}\left(=90^o\right)\)
\(\Rightarrow\widehat{EDM}+\widehat{EDH}=\widehat{FDB}+\widehat{FDH}\)
mà \(\widehat{EDM}=\widehat{FDB}\left(cmt\right)\)
Do đó \(\widehat{EDH}=\widehat{FDH}\)(2)
Từ (1) và (2) suy ra:
\(\widehat{EDH}+\widehat{EDM}=\widehat{FDH}+\widehat{KDM}\)
\(\Rightarrow\widehat{FDH}+\widehat{KDM}=90^o\)
Do đó: \(\widehat{EDH}+\widehat{EDM}+\widehat{FDH}+\widehat{KDM}=90^o+90^o\)
\(\Rightarrow\widehat{FDK}=180^o\)
Vậy ba điểm F;D;K thẳng hàng
Chúc bạn học tốt!!!
Có gì đó không đúng.