Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCAB có CN/CA=CP/CB
nên NP//AB và NP=AB/2
=>NP//AM và NP=AM
=>AMPN là hình bình hành
mà góc MAN=90 độ
nên AMPN là hình chữ nhật
b: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=108/15=7,2(cm)

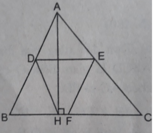
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

a: Ta có: H và M đối xứng nhau qua AB
nên BA là đường trung trực của HM
Suy ra: AM=AH(1)
ta có: H và N đối xứng nhau qua AC
nên AC là đường trung trực của HN
Suy ra: AH=AN(2)
Từ (1) và (2) suy ra AM=AN=AH

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
b: BC=10cm
AH=4,8cm
BH=3,6cm
CH=6,4cm

1) Vì I là trung điểm của AB ; K là trung điểm của AC => IK là đường trung bình của Tam giác ABC
=> IK // BC hay tứ giác IKCB là hình thang
2) Vì I là trung điểm của AB ; N là trung điểm của BH => IN là đường trung bình của tam giác ABH
=> IN = \(\frac{1}{2}\) AH (1)
Vì K là trung điểm của AC ; M là trung điểm của HC => KM là đường trung bình của tam giác ACH
=> KM = \(\frac{1}{2}\) AH
Từ (1); (2) => \(IN=KM=\frac{1}{2}AH\)
Xét ΔAHC có
I là trung điểm của AH
N là trung điểm của AC
DO đó: IN là đường trung bình của ΔAHC
Suy ra: \(IH=3cm\)