Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8:
a) Xét tứ giác BFEC có
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}\)
nên BCEF là tứ giác nội tiếp
Xét tứ giác CDHE có
\(\widehat{HDC}+\widehat{HEC}=180^0\)
Do đó: CDHE là tứ giác nội tiếp

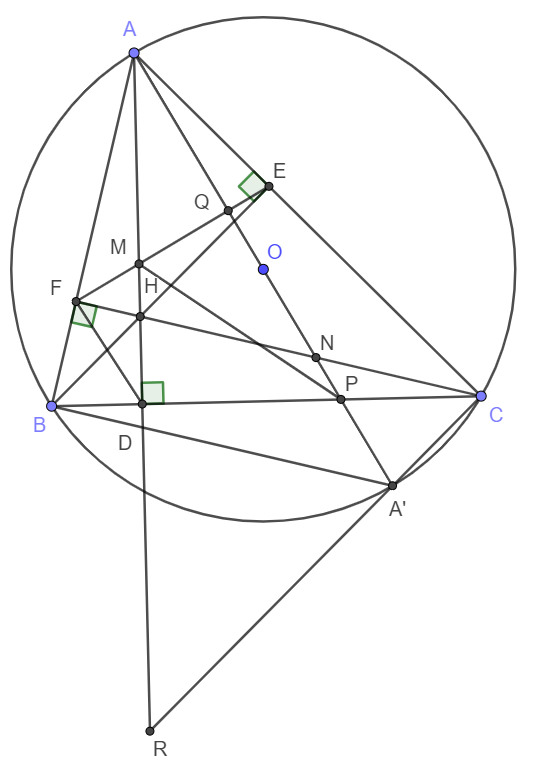
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm

c) Gọi K là giao điểm của EF và AH, I và G lần lượt là trung điểm của EF và AH.
Ta thấy \(\left(DKHA\right)=-1\),G là trung điểm của HA => \(DK.DG=DH.DA=DB.DC\)
=> K là trực tâm của \(\Delta\)BGC => CK vuông góc BG
Vì CK vuông góc BG, BH vuông góc AC nên \(\widehat{ACK}=\widehat{HBG}\)(1)
Ta có \(\widehat{AEF}=\widehat{ABC}=\widehat{APC}\)=> (P,K,E,C)cyc => \(\widehat{ACK}=\widehat{APM}=\widehat{ABM}\)(2)
Lại có \(\Delta\)BFE ~ \(\Delta\)BHA, I và G lần lượt là trung điểm của FE và HA => \(\widehat{HBG}=\widehat{FBI}\)(3)
Từ (1);(2);(3) suy ra \(\widehat{ABM}=\widehat{FBI}\), mà BF trùng BA nên B,I,M thẳng hàng hay BM chia đôi EF.
Bạn tham khảo thêm cách này:
Ta có \(\widehat{FGE}+\widehat{FDE}=2\widehat{BAC}+(180^0-2\widehat{BAC})=180^0\)
=> Tứ giác FGED nội tiếp, vì DG là phân giác góc EDF nên \(\Delta\)DFK ~ \(\Delta\)DGE (g.g)
=> \(DK.DG=DE.DF\)
Lại có \(\Delta\)DBF ~ \(\Delta\)DEC (g.g) => \(DE.DF=DB.DC\)
Suy ra \(DK.DG=DB.DC\)=> \(\Delta\)BDK ~ \(\Delta\)GDC (c.g.c)
=> \(\widehat{DBK}=\widehat{DGC}\). Mà \(\widehat{DGC}\)phụ \(\widehat{GCB}\)nên BK vuông góc GC
Vậy K là trực tâm tam giác BGC.