Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do 2 đường cao BD và CE cắt nhau tại H => H là trực tâm của tam giác ABC. Nối A với H sao cho AH cắt BC tại F, ta có AF là đường cao thứ 3 của tam giác ABC => \(AF\perp BC\)
Vì \(\Delta ABF\) vuông tại D \(\Rightarrow\widehat{BAF}+\widehat{ABF}=90^0\) hay \(\widehat{ABF}=\widehat{HAE}\) (1)
\(\Delta BEC\) vuông tại E \(\Rightarrow\widehat{BCE}+\widehat{CBE}=90^0\) hay \(\widehat{ABF}+\widehat{KCB}=90^0\) (2)
Từ (1) và (2) => \(\widehat{HAE}=\widehat{KCB}\) (3)
Ta dễ chứng minh được \(\Delta KAE=\Delta HAE\left(c-g-c\right)\)
\(\Rightarrow\widehat{KAE}=\widehat{HAE}\) hay \(\widehat{KAB}=\widehat{HAE}\) (4)
Từ (3) và (4) \(\Rightarrow\widehat{KAB}=\widehat{KCB}\)
Vậy...

AH cắt BC tại M.
Xét \(\Delta ABC\) có 2 đường cao BD và CE cắt nhau tại H
=> H là trực tâm của tam giác ABC
=> \(AH⊥BC\)
=> \(\Delta ABM\)vuông tại M
=> \(\widehat{BAM}+\widehat{ABM}=90^o\)
Mà \(\widehat{KCB}+\widehat{ABM}=90^o\)
Nên \(\widehat{BAM}=\widehat{KCB}\)
Ta có: AK = AH ( A thuộc đường trung trực của đoạn HK)
=> \(\Delta AKH\)cân tại A
Mà AE là đường trung tuyến nên cũng là đường phân giác
=> \(\widehat{KAB}=\widehat{BAM}\)
Mà \(\widehat{KCB}=\widehat{BAM}\)
Nên \(\widehat{KAB}=\widehat{KCB}\)\(\left(đpcm\right)\)

tự kẻ hình
a) xét tam giác BEC và tam giác CDB có
BC chung
BEC=CDB(=90 độ)
ABC=ACB( tam giác ABC cân A)
=> tam giác BEC= tam giác CDB(ch-gnh)
=> BD=CE( hai cạnh tương ứng)
b) từ tam giác BEC= tam giác CDB=> DBC=ECB(hai góc tương ứng)
=> tam giác HBC cân H
c) đặt O là giao điểm của AH với BC
vì AH,BD,CE cùng giao nhau tại H mà BD, CE là đường cao=> AH là đường cao ( 3 đường cao cùng đi qua một điểm)
vì HBC cân H=> HB=HC
xét tam giác HOB và tam giác HOC có
HB=HC(cmt)
HBO=HCO(cmt)
HOB=HOC(=90 độ)
=> tam giác HOB= tam giác HOC(ch-gnh)
=> BO=CO( hai cạnh tương ứng)
=> AH là trung trực của BC
d) xét tam giác CDB và tam giác CDK có
BD=DK(gt)
CDB=CDK(=90 độ)
DC chung
=> tam giác CDB= tam giác CDK(cgc)
=> CBD=CKD( hai cạnh tương ứng)
mà CBD=BCE=> CKD=BCE
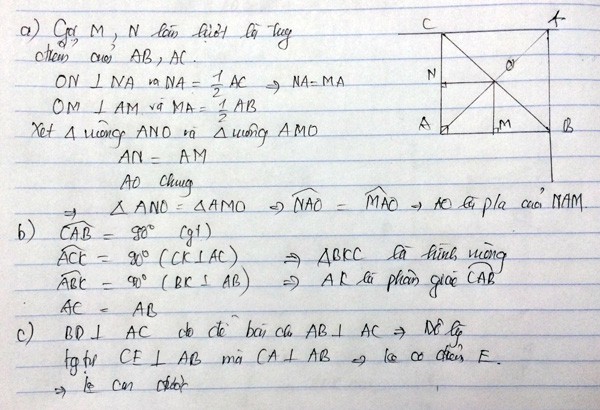
vÌ H LÀ giao điểm củabd và ce => h là trực tâm=>ah vuông góc bc .
gọi e là giao điểm ah vf bc. ta có góc bae +abc=90
góc abc+kcb=90
=> bah=kcb 1
ab là đường trung trực hk
=> ak=ah=> tam giác akh cân => ab đồng thời là đương phân giác => kab=hab 2
tuw1 vaf2 => kab=kcb