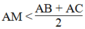VS
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2022
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
H
8 tháng 12 2021
Tham Khảo e nhá chj ngu ném ko bik làm☹
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-m-la-trung-diem-bc-chung-minh-ab2-ac2-2am2-bc22.249563555147
10 tháng 12 2021
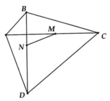
Kẻ AH vuông góc BC.
Xét tam giác AHM vuông tại H (^AHM = 900) có:
AM2 = AH2 + HM2 (định lý Pytago).
Xét tam giác AHB vuông tại H (^AHB = 900) có:
AB2 = AH2 + BH2 (định lý Pytago).
Xét tam giác AHC vuông tại H (^AHC = 900) có:
AC2 = AH2 + CH2 (định lý Pytago).
Ta có: BH = BM - HM.
CH = CM + HM.
Vì M là trung điểm của BC (gt) => BM = CM; BM = \(\dfrac{BC}{2}\) => BM2 = \(\dfrac{BC^2}{4}\).
Ta có: AB2 + AC2 = AH2 + BH2 + AH2 + CH2.
AB2 + AC2 = AH2 + AH2 + BH2 + CH2.
= 2AH2 + (BM - HM)2 + (CM + HM)2.
= 2AH2 + BM2 - 2BM.HM + HM2 + CM2 + 2CM.HM + HM2.
= 2AH2 + BM2 - 2BM.HM + HM2 + BM2 + 2BM.HM + HM2.
= 2AH2 + 2HM2 + 2BM2.
= 2(AH2 + HM2) + 2\(\dfrac{BC^2}{4}\).
AB2 + AC2 = 2AM2 + \(\dfrac{BC^2}{2}\) (đpcm).
vuông tại B chọn câu đúng 
PT
1
CM
1 tháng 6 2018
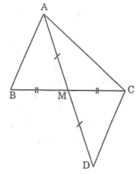
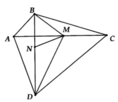
Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (hai cạnh tương ứng)
Trong ΔACD, ta có: AD < AC + CD
(bất đẳng thức tam giác)
Suy ra: AD < AC + AB
Mà AD = AM + MD = 2AM
Suy ra: 2AM < AC + AB hay 
