Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/90300865_513759882662331_7933478677944205312_n.jpg?_nc_cat=103&_nc_sid=b96e70&_nc_ohc=3FRJRAk93ccAX_g-K3Y&_nc_ht=scontent-hkt1-1.xx&oh=ecbc1515b5973f61bb5467b90f15ad1d&oe=5E9696F5
mình chụp ảnh r nhá . cậu tải zề zà quay lại chiều sao cho thấy nhá
nếu cần thì bảo mình ghi ra cho

a, Xét hai tam giác ABH và tam giác ADH có
BH=HD(giả thiết)
góc BHA=góc DHA(=90 độ)
AH chung
Suy ra ABH=ADH(dpcm)
b,c,d dài qúa mik ko ghi nổi bạn thông cảm nhé^^

a) Xét \(\Delta AIB\),\(\Delta AIC\) có: ^BAI=^CAI (gt) , AI chung, AB=AC
=>\(\Delta AIB\)=\(\Delta AIC\)(c.g.c)
b) Xét\(\Delta AMD\), \(\Delta CMB\) có: ^AMD=^BMC (2 goc đối điỉnh)
AM=MC(gt) ; BM=MD(gt)
=>\(\Delta AMD\)=\(\Delta CMB\)(c.g.c)
=> AD=BC ; BD=AC
Xét \(\Delta ABC\) => AB+BC>AC ( bđt trong tam giác)
mà AC=BD => AB+BC>BD
c) xét \(\Delta AHM\),\(\Delta CKM\) (^AHM=^CKM=90o) có: AM=MC(gt) , ^AMH=^CMK ( 2gocs dd)
=>\(\Delta AHM\)=\(\Delta CKM\)
=>AH=CK
=>AH+CK=2AH
Xét \(\Delta AHM\) vuông tại H:=> ^AMH< ^AHM
=> AM>AH
=>2AM>2AH
mà 2AM=AC(gt) 2AH= AH +CK
=>AC>AH+CK

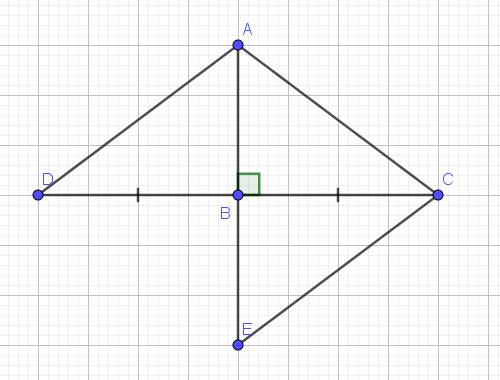
a) Xét hai tam giác vuông: \(\Delta ABD\) và \(\Delta ABC\) có:
AB chung
BD = BC (gt)
\(\Rightarrow\Delta ABD=\Delta ABC\) (hai cạnh góc vuông)
b) Do \(\Delta ABD=\Delta ABC\) (cmt)
\(\Rightarrow\widehat{ADB}=\widehat{ACB}\) (hai góc tương ứng)
Ta có: CE // AD (gt)
\(\Rightarrow\widehat{BCE}=\widehat{ADB}\) (so le trong)
\(\Rightarrow\widehat{BCE}=\widehat{ACB}\)
Xét hai tam giác vuông: \(\Delta CBA\) và \(\Delta CBE\) có:
BC là cạnh chung
\(\widehat{ACB}=\widehat{BCE}\) (cmt)
\(\Rightarrow\Delta CBA=\Delta CBE\) (cạnh góc vuông-góc nhọn kề)
\(\Rightarrow CA=CE\) (hai cạnh tương ứng)
\(\Delta ACE\) có CA = CE (cmt)
\(\Rightarrow\Delta ACE\) cân tại C

t lười vẽ hình lắm, vô cùng xin lỗi :(
a) Vì ∆ ABC cân tại A nên AH vừa là đường cao, vừa là trung tuyến => HB = HC = 12:2 = 6
Áp dụng định lí Py-ta-go cho ∆ AHB, ta được: AH2 + BH2 = AB2 => AB2 = 122 + 92 = 225 = 152 => AB = 15 = AC
=> PABC = AB + AC + BC = 15 + 15 + 18 = 48
b) Vì BM = CN (gt) ; HB = HC (cmt) => HB + BM = HC + CN => HM = HN => AH là trung tuyến của ∆ AMN (1)
Lại có: AH ┴ BC hay AH ┴ MN => AH là đường cao của ∆ AMN (2)
Từ (1) và (2) =>∆ AMN cân tại A
c) Xét ∆ BIM và ∆ CKN vuông tại I và K có:
MB = NC (gt) ; ^KNC = ^IMB (∆AMN cân tại A) => ∆ BIM = ∆ CKN ( ch - gn ) => MI = KN
Mà AM = AN (∆AMN cân tại A) => AI = AK => ∆ AIK cân tại A
=> ^AIK = ^AKI = ( 180o - ^MAN ) : 2 = ^AMN = ^ANM => IK // MN (đồng vị) hay IK // BC
d) Vì IK // MN => ^IKN = ^KCN (slt) ; ^KIB = ^IBM (slt)
Lại có: ^IBM = ^KCN ( vì ∆BIM=∆CKN ) => ^IKN = ^KIB hay ^OIK = ^OKI => ∆OKI cân tại O => OK = OI
Xét ∆ AIO và ∆ AKO có:
AI = AK ( ∆AIK cân tại A) ; OK = OI (cmt) ; AO (chung) => ∆ AIO = ∆ AKO ( c-c-c )
=> ^OAI = ^OAK (3)
Vì ∆AMN cân tại A => AH là phân giác của ∆AMN.=> ^HAM = ^HAN hay ^HAI = ^HAK (4)
Từ (3) và (4) => A, O, H thẳng hàng.
Ya, that's it!
cậu lm đc ch cs thể giải cho mình đc hông