Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: AC=12cm
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
b:
Ta có: AB và AE là hai tia đối nhau
=>A nằm giữa B và E
mà AB=AE
nên A là trung điểm của BE
Xét ΔCBE có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBE cân tại C
c: Ta có: ΔCBE cân tại C
mà CA là đường cao
nên CA là phân giác của góc ECB
Xét ΔCIA vuông tại I và ΔCHA vuông tại H có
CA chung
\(\widehat{ICA}=\widehat{HCA}\)
Do đó: ΔCIA=ΔCHA
d: Ta có: ΔCIA=ΔCHA
=>CI=CH
Xét ΔCEB có \(\dfrac{CI}{CE}=\dfrac{CH}{CB}\)
nên HI//EB

b) Ta có: ΔBAD=ΔBED(cmt)
nên DA=DE(hai cạnh tương ứng)
Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(Đpcm)
Sửa đề: BA=BE
a) Xét ΔBAD và ΔBED có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBAD=ΔBED(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE⊥BC(đpcm)

a: Xét ΔAIK vuông tại A và ΔDIC vuông tại D có
IA=ID
\(\widehat{AIK}=\widehat{DIC}\)
Do đó: ΔAIK=ΔDIC
Suy ra: IK=IC
hay ΔIKC cân tại I
b: Xét ΔBKC có BA/AK=BD/DC
nên AD//KC
c: Ta có: BK=BC
nên B nằm trên đường trung trực của KC(1)
ta có: IK=IC
nên I nằm trên đường trung trực của KC(2)
Ta có: MK=MC
nên M nằm trên đường trung trực của KC(3)
Từ (1), (2)và (3) suy ra B,I,M thẳng hàng

Bạn chú ý viết cách phần cho và phần yêu cầu.
a/ Xét t/g ABI và t/g ADI có
AI : chung
\(\widehat{BAI}=\widehat{CAI}\) (AI là pg góc BAC)
AB = AD (GT)
=> t/g ABI = t/g ADI (c.g.c)
=> BI = DI (2 cạnh t/ứ)
b/ Có t/g ABI = t/g ADI
=> \(\widehat{ABI}=\widehat{ADI}\)(2 góc t/ứ)
=> \(180^o-\widehat{ABI}=180^o-\widehat{ADI}\)
=> \(\widehat{IBK}=\widehat{IDC}\) Xét t/g BIK và t/g DIC có
\(\widehat{IBK}=\widehat{IDC}\)
IB = DI (cmt)
\(\widehat{BIK}=\widehat{DIC}\)(đối đỉnh)
=> t/g BIK = t/g DIC (g.c.g)
c/ Có t/g BIK = t/g DIC
=> BK = DC (2 cạnh t/ứ) => AB + BK = DC + AD
=> AK = AC
=> t/g AKC cân tại A
Mà AI là pg góc BAC (K thuộc AB)
=> AI đồng thời là đường cao t/g AKC
=> AI ⊥ KC Mà BH ⊥ KC
=> AI // BH
bạn tự vẽ hình nhá
Vì AI là tia phân giác ⇔ \(\widehat{BAI}=\widehat{DAI}=\dfrac{\widehat{BAC}}{2}\)
a) xét Δ ABI và ΔADI, có:
AB=AD
\(\widehat{BAI}=\widehat{DAI}\) (cmt)
AI chung
⇒Δ ABI =Δ ADI (c.g.c)
⇒BI=DI (2 cạnh t/ứng) (đpcm)
b) Do Δ ABI =Δ ADI (cmt) ⇒ \(\widehat{ABI}=\widehat{ADI}\)
Có: \(\widehat{ABI}+\widehat{IBK}\) =1800 (2 góc kề bù)
\(\widehat{ADI}+\widehat{IDC}\) =1800 (2 góc kề bù)
Mà \(\widehat{ABI}=\widehat{ADI}\) (cmt) ⇒ \(\widehat{IBK}=\widehat{IDC}\)
Vì \(\widehat{BIK}\) và \(\widehat{DIC}\) là 2 góc đối đỉnh ⇒ \(\widehat{BIK}\) =\(\widehat{DIC}\)
xét Δ BKI và Δ DCI có:
\(\widehat{IBK}=\widehat{IDC}\) (cmt)
BI=ID (cmt)
\(\widehat{BIK}\) =\(\widehat{DIC}\) (cmt)
⇒Δ BKI = Δ DCI (g.c.g) (đpcm)
c) Từ Δ BKI = Δ DCI (cmt) ⇒ BK=DC
Có AB=AD (gt) ; BK=DC (cmt)
⇔AB+BK=AD+DC
⇔AK=AC
⇒Δ ACK cân tại A.
Mà AI là phân giác của \(\widehat{KAC}\) (gt)
⇒AI vừa là đường phân giác vừa là đường cao của Δ ACK.
⇒AI ⊥ CK. mà BH ⊥ CK (gt)
⇒AI // BH (đpcm)
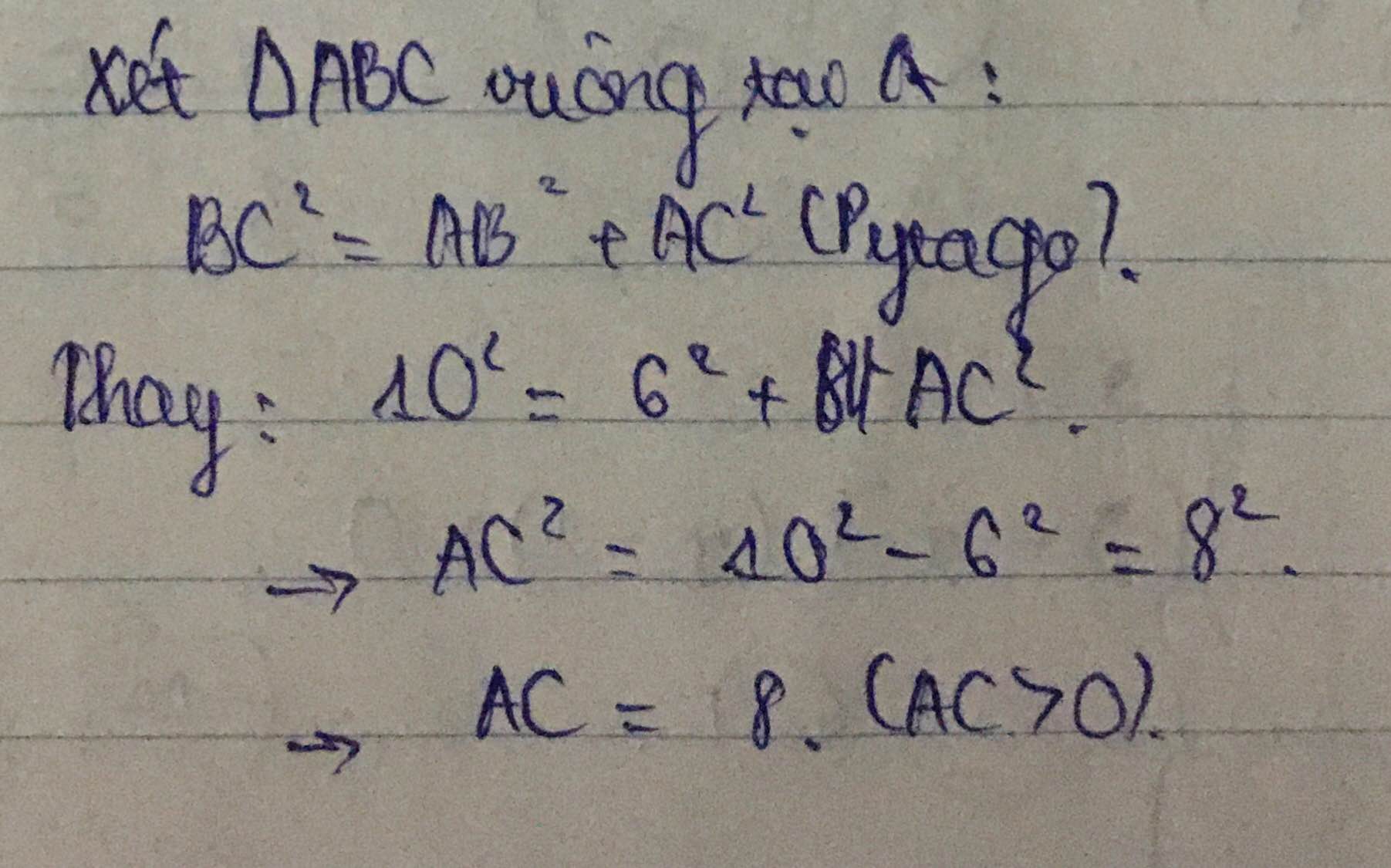




a) Xét \(\Delta ABI\) và \(\Delta DBI:\)
AB = DB (gt).
\(\widehat{ABI}=\widehat{DBI}\) (BI là phân giác \(\widehat{ABC}).\)
BI chung.
\(\Rightarrow\Delta ABI=\Delta DBI\left(c-g-c\right).\\ \Rightarrow\widehat{BAI}=\widehat{BDI}=90^o.\\ \Rightarrow DI\perp BC.\)
b) Xét \(\Delta BCE:\)
ED là đường cao \(\left(ED\perp BC\right).\)
CA là đường cao \(\left(CA\perp AB\right).\)
I là giao điểm của ED và CA.
\(\Rightarrow\) I là trực tâm.
\(\Rightarrow\) BI là đường cao.
Xét \(\Delta BCE:\)
BI là đường cao (cmt).
BI là phân giác (gt).
\(\Rightarrow\) \(\Delta BCE\) cân tại B.
d) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow10^2=8^2+AC^2.\\ \Leftrightarrow AC=6\left(cm\right).\)
mik chx hok đường cao và trực tâm nếu câu b bn còn cách giải kahcs thì mik cảm ơn