Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đề bị sai nha các bạn...
câu b mk lộn
b/ gọi F là trung điểm của CE. cm A, M, F thẳng hàng.

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1/2 BC
Vì G là trọng tâm của ∆ ABC nên AG = 2/3 AM AM => AG = 2/3.1/2 BC
=> AG = 1/3 BC = 1/3.5 = 1.7cm

a) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời cũng là trung tuyến.
\(\Rightarrow BH=\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có:
\(AH^2+BH^2=AB^2\) (Định lý Py-ta-go)
\(\Rightarrow AH^2+3^2=5^2\)
\(\Rightarrow AH^2=5^2-3^2=26-9=16\)
Mà \(AH>0\Rightarrow AH=4\left(cm\right)\)
Vậy \(BH=3\) \(cm;\) \(AH=4\) \(cm.\)
b) G là trọng tâm \(\Delta ABC\), nên G nằm trên đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow G\in AH\)
\(\Rightarrow A,G,H\) thẳng hàng.
Vậy \(A,G,H\) thẳng hàng.
c) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời là phân giác góc BAC
\(\Rightarrow AG\) là phân giác góc BAC
\(\Rightarrow\) Góc BAG = góc CAG
Xét \(\Delta BAG\) và \(\Delta CAG\), ta có:
\(AB=AC\) ( \(\Delta ABC\) cân tại A)
Góc BAG = góc CAG (Chứng minh trên)
Cạnh AG chung
\(\Rightarrow\Delta BAG=\Delta CAG\left(c.g.c\right)\)
\(\Rightarrow\) Góc ABG = góc ACG (hai góc tương ứng)
Vậy góc ABG = góc ACG.

Đáp án A
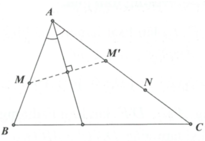
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
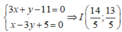
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
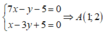
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
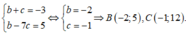
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()


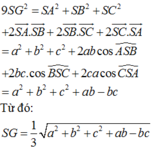
AG =\(\dfrac{2}{3}AM\\\)\(\Rightarrow AG=8\left(cm\right)\)
\(GM=\dfrac{1}{3}AM\Rightarrow GM=4\left(cm\right)\)
lp mấy r mà k làm đc bài này