
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


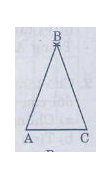
a) Vẽ đoạn thẳng AC= 3cm.
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 4cm và cung tròn C bán kính 4cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.
b) Tương tự cách vẽ ở câu a với các cung tròn tâm A, tâm C có cùng bán kính 3cm.


Chứng minh tam giác vuông:
Ứng dụng:
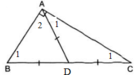
- Vẽ đường tròn (A, r) với r = AB/2; vẽ đường tròn (B, r).
- Gọi C là giao điểm của hai cung tròn nằm ở phía trong tờ giấy.
- Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
Thật vậy: ΔABD có AC là trung tuyến ứng với BD (BC = CD) và AC = BC = CD.
=> AC = BD => ∆ABD vuông tại A.

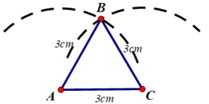
Vẽ đoạn thẳng AC = 3cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 3cm và cung tròn C bán kính 3cm
- Hai cung tròn trên cắt nhau tại B
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.


Cách 1:
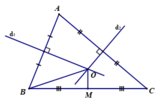
Gọi trung điểm BC là M
Ta kẻ xy qua M vuông góc với BC
Cách 2:
Từ B, C vẽ 2 cung tròn có bán kính \(R \ge \dfrac{1}{2}BC \)
2 cung tròn giao nhau tại 2 điểm M, N
Kẻ đường thẳng xy đi qua 2 điểm M, N. Ta được đường trung trực xy đi qua chúng