Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

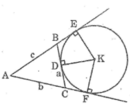
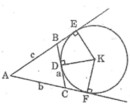
Gọi D là tiếp điểm của đường tròn (K) với cạnh BC.
Theo tính chất hai tiếp tuyến cắt nhau ta có:
BE = BD; CD = CF
AE = AB + BE
AF = AC + CF
Suy ra: AE + AF = AB + BE + AC + CF
= AB + AC + (BD + DC)
= AB + AC + BC = c + b + a
Mà: AE = AF (tính chất hai tiếp tuyến cắt nhau)
Suy ra: A E = A F = a + b + c 2

gọi D là tiếp điểm của đường tròn (K) trên BC . ta có DB = BE ; CD = CF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AB + BE = c + BD
AF = AC + CF = b + CD
\(\Rightarrow\) AE + AF = b + c + (BD + CD)
= a + b + c
ta lại có AE = AF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AF = \(\dfrac{a+b+c}{2}\) (đpcm)
b) BE = AE - AB = \(\dfrac{a+b+c}{2}\) - c = \(\dfrac{a+b-c}{2}\) (đpcm)
c) CF = AF - AC = \(\dfrac{a+b+c}{2}\) -b = \(\dfrac{a+c-b}{2}\) (đpcm)

Ta có: AE’ = AF’, BD’ = BF’, CD’ = CE’ (tính chất hai tiếp tuyến cắt nhau).
Suy ra
AE’ + AF’ = (AC + CE’) + (AB + BF’)
= (AC + CD’) + (AB + BD’) = AC + BC + AB = 2p.
Do đó: AE’ = AF’ = p.

cho em xin lỗi em đánh thiếu. đường tròn bàng tiếp trong góc C tiếp xúc với BC tại M


Ta có: B E = A E - A B = a + b + c 2 - c = a + b - c 2