Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Xét ∆AMN và ∆CKN có:
AN = NC (gt)
\(\widehat{ANM}=\widehat{CNK}\)( đối đỉnh)
NM = NK (gt)
=>∆AMN = ∆CKN (c-g-c)
+ Cm được ∆ANK = ∆CNM
=> Góc NAK = góc NCM ( tương ứng)
=> AK // MC ( so le trong =)
Vì∆AMN = ∆CKN => MA = KC và góc AMN = góc CKN
+ XÉt∆MNB và ∆KND có :
MN = KN(gt)
\(\widehat{BMN}=\widehat{DKN}\)
MB = KD ( vì MB = MA; MA = KC; KC = KD)
=> ∆MNB = ∆KND (c-g-c) (1)
=> NB = ND
và góc MNB = góc KND mà M,N,K thẳng hàng
=> B,N,D thẳng hàng
Từ(1),(2) => N là trung điểm BD

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AMCE có
N là trung điểm của AC
N là trung điểm của ME
Do đó: AMCE là hình bình hành
Suy ra: AE=CM

a) Ta có: \(AP=BP=\dfrac{AB}{2}\)(P là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AP=BP=AN=NC
Xét ΔABN và ΔACP có
AB=AC(ΔABC cân tại A)
\(\widehat{BAN}\) chung
AN=AP(cmt)
Do đó: ΔABN=ΔACP(c-g-c)
Suy ra: BN=CP(hai cạnh tương ứng)
b) Xét ΔMNC và ΔINA có
MN=IN(gt)
\(\widehat{MNC}=\widehat{INA}\)(hai góc đối đỉnh)
NC=NA(N là trung điểm của AC)
Do đó: ΔMNC=ΔINA(c-g-c)
Suy ra: MC=IA(hai cạnh tương ứng)
Xét ΔANM và ΔCNI có
AN=CN(N là trung điểm của AC)
\(\widehat{ANM}=\widehat{CNI}\)(hai góc đối đỉnh)
NM=NI(gt)
Do đó: ΔANM=ΔCNI(c-g-c)
Suy ra: AM=CI(hai cạnh tương ứng)
Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
hay \(\widehat{AMC}=90^0\)(1)
Xét ΔAMC và ΔCIA có
AC chung
AM=CI(cmt)
MC=IA(cmt)
Do đó: ΔAMC=ΔCIA(c-c-c)
Suy ra: \(\widehat{AMC}=\widehat{CIA}\)(hai góc tương ứng)(2)
Từ (1) và (2) suy ra \(\widehat{AIC}=90^0\)
Vậy: \(\widehat{AIC}=90^0\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
MB=MC
Do đó: ΔABM=ΔACM

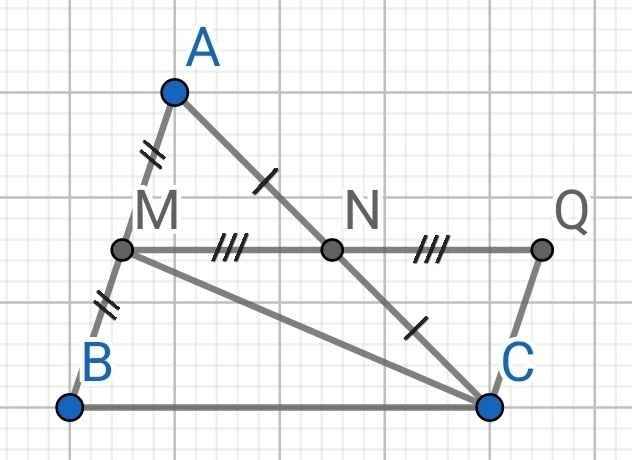
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC
cau hoi dau chung minh cai gi ban
a,Chứng minh : AD // MC
b,Chứng minh : BC = 2MN
Giải :
Bạn tự vẽ hình nhé
a, C1 : Tứ giác AMCD có 2 đường chéo cắt nhau tại trung điểm mỗi đường
\(\Rightarrow\) Tứ giác AMCD là hình bình hành
\(\Rightarrow\) AD // MC
C2:\(\Delta NAD=\Delta NCM\left(c.g.c\right)\)
\(\Rightarrow\widehat{NAD}=\widehat{NCM}\)( 2 góc tương ứng )
Mà \(\widehat{NAD}\)và \(\widehat{NCM}\)ở vị trí so le trong
\(\Rightarrow\)AD // MC ( Dấu hiệu )
b,C1: Vì tứ giác AMCD là hình bình hành ( chứng minh trên )
\(\Rightarrow\)CD // AM và CD = AM
Mà AM = MB và đường thẳng AM và đường thẳng MB trùng nhau
\(\Rightarrow\)CD // MB và CD = MB
\(\Rightarrow\)MBCD là hình bình hành ( vì có hai cạnh đối song song và bằng nhau )
\(\Rightarrow\)BC = MD
Mà MD = 2MN
\(\Rightarrow\)BC = 2MN
C2 : \(\Delta NAD=\Delta NCM\)
\(\Rightarrow AD=MC\)( 2 cạnh tương ứng )
Mà AD // MC
\(\Rightarrow\)Tứ giác AMCD là hình bình hành
\(\Rightarrow\)CD // AM và CD = AM
Mà AM = MB và đường thẳng AM và MB trùng nhau
\(\Rightarrow\)CD // MB và CD = MB
\(\Rightarrow\)MBCD là hình bình hành
\(\Rightarrow\)BC = MD
Mà MD = 2MN
\(\Rightarrow\)BC = 2MN