Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì DF // AE (DF//AB; E \(\in AB\)) nên \(\widehat{AEF}=\widehat{EFD}\) (2 góc so le trong)
Hay \(\widehat{AEI}=\widehat{IFD}\) ( I \(\in EF\) )
Xét \(\Delta AEI\) và \(\Delta DFI\) có:
\(\widehat{AEI}=\widehat{IFD}\) (c/m trên)
IE=IF(I là trung điểm của EF)
\(\widehat{AIE}=\widehat{DIF}\) (2 góc đối đỉnh)
=> \(\Delta AEI=\Delta DFI\left(g.c.g\right)\)
=> IA=IB( 2 cạnh tương ứng). Mà I nằm giữa A và B
=> I là trung điểm của AB

a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a,
Ta có : D là trung điểm của BC
Mà Δ ABC cân tại A
=> AD là đường cao
=> AD là đường phân giác \(\widehat{BAC}\)
Xét Δ ABD và Δ ACD, có :
\(\widehat{ADB}=\widehat{ADC}=90^o\)
\(\widehat{ABD}=\widehat{ACD}\) (Δ ABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ ABD = Δ ACD (g.g.g)
b, Ta có : AD là đường cao (cmt)
=> AD ⊥ BC
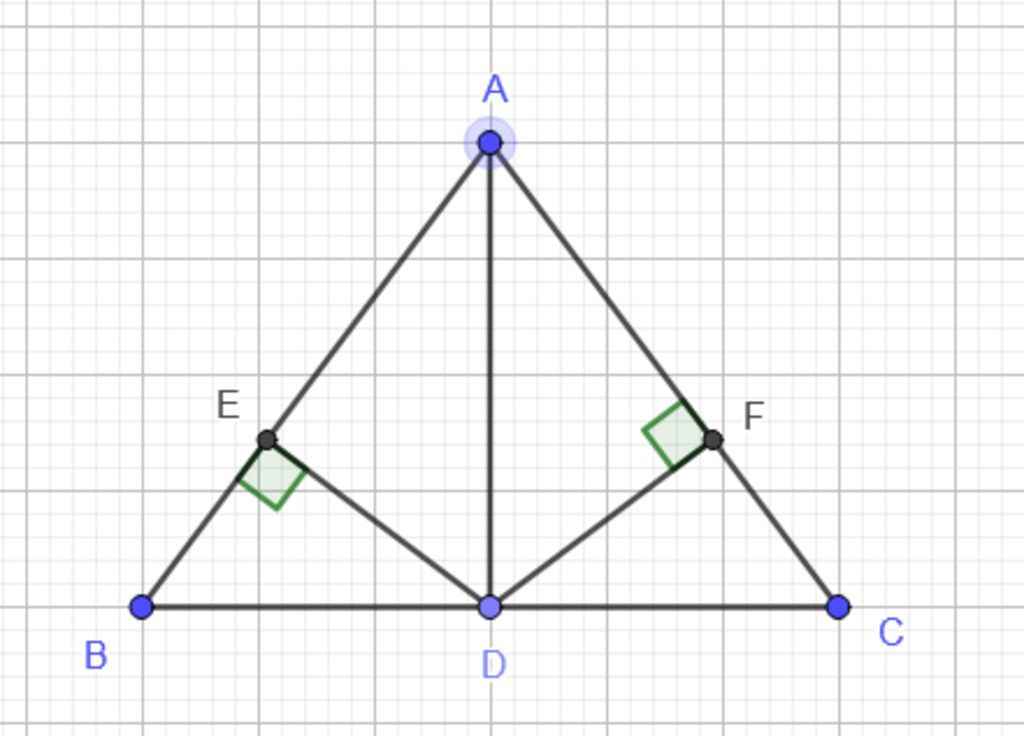
c, Xét Δ AED và Δ AFD, có :
AD là cạnh chung
\(\widehat{AED}=\widehat{AFD}=90^o\)
\(\widehat{EAD}=\widehat{FAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ AED = Δ AFD (g.c.g)
=> ED = FD
Xét Δ EBD vuông tại E và Δ FCD vuông tại F, có :
ED = FD
DB = DC (D là trung điểm BC)
=> Δ EBD = Δ FCD (ch - cgv)
d, Ta có : BC = 2DC (D là trung điểm BC)
=>12 = 2DC
=> DC = 6 (cm)
Xét Δ ADC vuông tại D, có :
\(AC^2=AD^2+DC^2\) (định lí Py - ta - go)
=> \(10^2=AD^2+6^2\)
=> \(64=AD^2\)
=> AD = 8 (cm)

a)Xét \(\Delta ABD\) và \(\Delta ACD\) có :
\(BD=DC\)
\(\widehat{ABD}=\widehat{ACD}\left(\Delta ABCcân\right)\)
AB= AC
=> \(\Delta ABD\) = \(\Delta ACD\) (c-g-c)
b) Vì \(\Delta ABC\) cân tại A nên AD vừa là đường trung tuyến vừa là đường cao
=> \(AD\perp BC\)
*Nếu chx học cách trên thì bạn xem cách dưới đây"
Vì \(\Delta ABD\) = \(\Delta ACD\) nên \(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^o\)
=> \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^o}{2}=90^o\)
=> \(AD\perp BC\)
c)Xét \(\Delta EBD\) vuông tại E và \(\Delta FCD\) vuông tại F có :
\(\widehat{EBD}=\widehat{FCD}\)
\(BD=CD\)
=> \(\Delta EBD=\Delta FCD\left(ch-gn\right)\)
d) Vì D là trung điểm của BC nên \(DC=\dfrac{BC}{2}=\dfrac{12}{2}=6cm\)
Xét \(\Delta ADC\) vuông tại D có :
\(AC^2=AD^2+DC^2\)
\(100=AD^2+36\)
\(AD^2=100-36\)
\(AD^2=64\)
AD=8 cm

*Tự vẽ hình
a) Có : DE//BC(GT)
EF//AB(GT)
=> BDEF là hình bình hành
=> BD=EF
Mà : AD=DB(GT)
=> AD=EF (đccm)
b) Ta có : AD=DB(GT)
DE//BC (GT)
=> DE là đường trung bình của tam giác ABC
=> AE=EC
Có : AE=EC(cmt)
EF//AB(GT)
=> EF là đường trung bình của tam giác ABC
=> BF=FC
Mà : BF=DE(BDEF-hình bình hành)
=> FC=DE
Xét tam giác ADE và EFC có :
AE=EC(cmt)
AD=EF(cm ý a)
DE=FC(cmt)
=> Tam giác ADE=EFC(c.c.c)
c) Đã chứng minh ở ý b
*Cách khác:
Giải:
Hình bạn tự vẽ nhé.
a) Ta có: BD // EF (vì AB /// EF)
=> Góc BDF = góc DFE (2 góc so le trong)
Vì DE // BC (gt)
nên góc EDF = góc BFD (2 góc so le trong)
Xét tam giác EDF và tam giác BDF có:
Góc BDF = góc DFE (chứng minh trên)
DF là cạnh chung
Góc EDF = góc BFD (chứng minh trên)
=> Tam giác DEF = tam giác FBD (g.c.g)
=> BD = EF ( 2 cạnh tương ứng) (đpcm)
Mà BD = AD (vì D là trung điểm của AB)
=> AD = EF (đpcm)
b) Ta có: AB // EF (gt)
=> Góc A = góc CEF (2 góc đồng vị)
Lại có: tam giác DEF = tam giác FBD (chứng minh trên)
=> Góc DEF = góc B (2 góc tương ứng) (1)
Mà DE // BC (gt)
=> Góc DEF = góc CFE (2 góc so le trong) (2)
Góc ADE = góc B (2 góc đồng vị)
Từ (1), (2) => Góc B = góc CFE
Mà góc B = góc ADE (chứng minh trên)
=> Góc ADE = góc CFE
Xét tam giác ADE và tam giác CEF có:
Góc CEF = góc A (chứng minh trên)
AD = EF (chứng minh trên)
Góc ADE = góc CFE (chứng minh trên)
=> Tam giác ADE = tam giác EFC (g.c.g) (đpcm)
c) Ta có: tam giác ADE = tam giác EFC (chứng minh trên)
=> AE = CE (2 cạnh tương ứng) (đpcm)

Xét ΔABC có
D là trung điểm của AB
DF//BC
Do đó: F là trung điểm của AC
Xét ΔABC có
D là trung điểm của AB
DE//AC
Do đó: E là trung điểm của BC
Xét ΔABC có
D là trung điểm của AB
E là trung điểm của BC
Do đó: DE là đường trung bình của ΔBCA

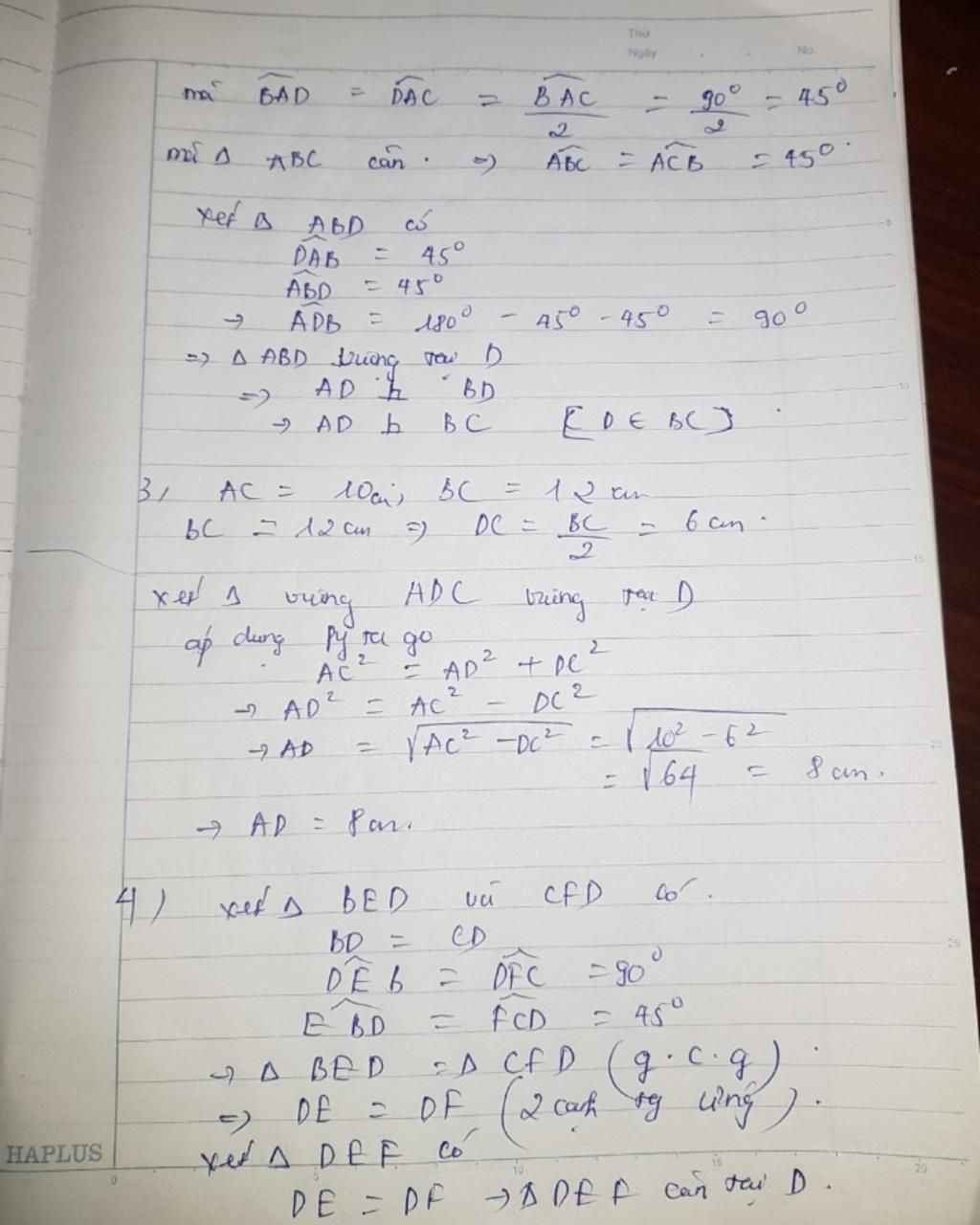
Vì DF // AE (DF//AB; E ∈AB∈AB) nên ˆAEF=ˆEFDAEF^=EFD^ (2 góc so le trong)
Hay ˆAEI=ˆIFDAEI^=IFD^ ( I ∈EF∈EF )
Xét ΔAEIΔAEI và ΔDFIΔDFI có:
ˆAEI=ˆIFDAEI^=IFD^ (c/m trên)
IE=IF(I là trung điểm của EF)
ˆAIE=ˆDIFAIE^=DIF^ (2 góc đối đỉnh)
=> ΔAEI=ΔDFI(g.c.g)ΔAEI=ΔDFI(g.c.g)
=> IA=IB( 2 cạnh tương ứng). Mà I nằm giữa A và B
=> I là trung điểm của AB
Vì DF // AE (DF//AB; E ∈AB∈AB) nên ˆAEF=ˆEFDAEF^=EFD^ (2 góc so le trong)
Hay ˆAEI=ˆIFDAEI^=IFD^ ( I ∈EF∈EF )
Xét ΔAEIΔAEI và ΔDFIΔDFI có:
ˆAEI=ˆIFDAEI^=IFD^ (c/m trên)
IE=IF(I là trung điểm của EF)
ˆAIE=ˆDIFAIE^=DIF^ (2 góc đối đỉnh)
=> ΔAEI=ΔDFI(g.c.g)ΔAEI=ΔDFI(g.c.g)
=> IA=IB( 2 cạnh tương ứng). Mà I nằm giữa A và B
=> I là trung điểm của AB