Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
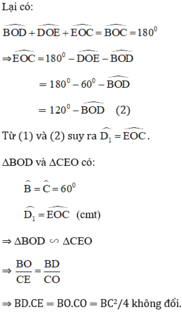
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 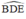
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).

Lời giải

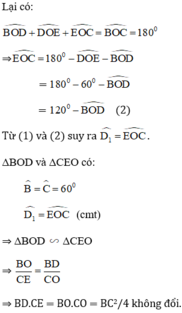
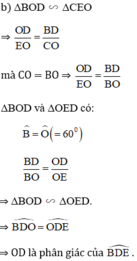
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 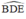
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).

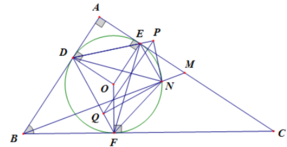
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.
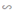 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.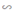 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
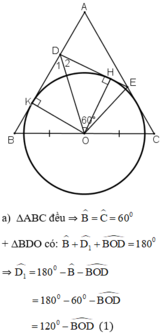
a, ^BOD + ^OBD = 120 = ^BOD + ^EOC (vì ^DOE = 60)
=> ^BDO = ^EOC
=> ∆BDO đồng dạng ∆COE
=> BD/BO = CO/CE
<=> BD.CE = BC²/4
b, DO/OE = BD/CO
<=> BO/OE = BD/OD
=> ∆BOD đồng dạng ∆OED
=> ^BDO = ^ODE
=> OD là tia phân giác của góc BDE
c, kẻ OI,OK lần lượt vuông góc với AB,DE
AB tiếp xúc với (O;OI)
có ∆IOD = ∆KOD (cạnh huyền góc nhọn)
=> OI = OK
mà OK ┴ DE
=> (O) luôn tiếp xúc với DE