Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 ▲vuông ADH và AHM, ta có:
HI và DI là đường trung tuyến của 2 ▲
⇒ DI = IH (=AI=IM)
⇒▲DIH cân tại I
Ta có: ▲ ADI cân tại I (DI=AI) ⇒ góc DIM = 2. góc IAD
▲ AHI cân tại I (HI=AI) ⇒ góc HIM = 2. góc IAH
⇒ góc DIH = 2.(góc IAD + góc HAI ) = 2. góc DAH= 2 . 30 độ = 60 độ ⇒ ▲ DIH đều
CMTT: ▲ IEH đều ⇒ DIEH là hình thoi
b) Gọi O là giao DE và HI và K là trung điểm AG, ta có IK là trung bình tam giác AMG và OG là trung bình tam giác KIH.
=> MG//IK và OG//IK
=> Tia MG và OG trùng nhau hay M, G, O thẳng hàng => MG, IH, DE đồng quy tại O
Chúc bạn học tốt☘

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
b: Xét tứ giác NKIM có
D là trung điểm của NI
D là trung điểm của KM
Do đó: NKIM là hình bình hành
mà NI vuông góc với KM
nên NKIM là hình thoi
c: Xét ΔABC có DN//AB
nên DN/AB=CN/CA=CD/CB
=>CN=1/2CA
hay N là trung điểm của AC
Xét ΔABC có DM//AC
nên BM/BA=BD/BC=1/2
hay BM=1/2BA
=>M là trung điểm của AB
Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên MA=MH
Ta có: ΔAHC vuông tại H
mà HN là đừog trung tuyến
nên HN=AN
Xét ΔMAN và ΔMHN có
MA=MH
AN=HN
MN chung
Do đó: ΔMAN=ΔMHN
Suy ra:góc MHN=90 độ

a) ADME là hình chữ nhật vì có 3 góc vuông: \(\widehat{A}\)= \(\widehat{D}\)= \(\widehat{E}\)= 900
b) Để ADME là hình vuông thì AM là phân giác \(\widehat{A}\)
Vậy M là giao đường phân giác góc A với BC thì ADME là hình vuông

a)\(\Delta ABC\) vuông tại A nên \(\widehat{BAC}=90^o\Rightarrow\widehat{DAE}=90^o\)
Có D là hình chiếu của M trên AB \(\Rightarrow MD\perp AB\Rightarrow\widehat{MDA}=90^o\)
Có E là hình chiếu của M trên AC \(\Rightarrow ME\perp AC\Rightarrow\widehat{AEM}=90^o\)
Xét tứ giác: \(ADEM\) có \(\left\{{}\begin{matrix}\widehat{DAE}=90^o\\\widehat{MDA}=90^o\\\widehat{AEM}=90^o\end{matrix}\right.\)
\(\Rightarrow\)Tứ giác ADEM là hình chữ nhật
Vậy tứ giác ADEM là hình chữ nhật.
b)\(\Delta ABC\) vuông tại A có AM là trung tuyến (M là trung điểm BC)
\(\Rightarrow AM=\dfrac{1}{2}BC\)
Mà \(AM=DE\) (tính chất hcn)
\(\Rightarrow DE=\dfrac{1}{2}BC\left(đpcm\right)\)
Bổ sung đề: Tam giác ABC vuông tại A
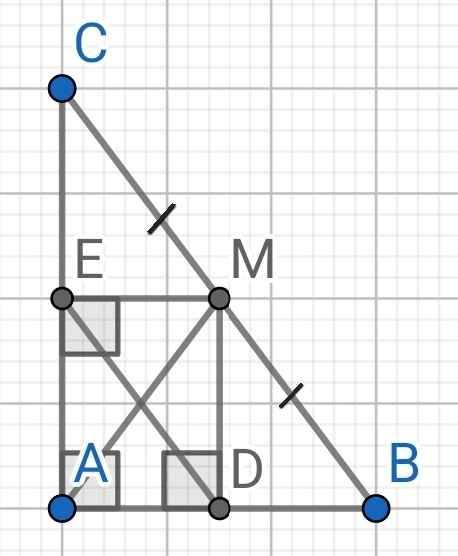 a) Xét tứ giác ADME có:
a) Xét tứ giác ADME có:
∠AEM = ∠EAD = ∠ADM = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do ADME là hình chữ nhật (cmt)
⇒ AM = DE (1)
Lại có:
AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BC/2 (2)
Từ (1) và (2) ⇒ DE = BC/2

A B C M H F D K I G
Câu a và b cô hướng dẫn:
a) Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
b) Tứ giác FDEA là hình bình hành nên AF // DE
c) Xét tam giác AFH có AD là đường cao đồng thời trung tuyến nên nó là tam giác cân.
Vậy thì AD là tia phân giác hay \(\widehat{FAD}=\widehat{DAH}\)
Do tam giác ABC vuông tại A, M là trung điểm BC nên MA = MB = MC hay \(\widehat{BAM}=\widehat{ABM}\)
Vậy thì \(\widehat{FAD}+\widehat{BAM}=\widehat{DAH}+\widehat{ABM}=90^o\)
\(\Rightarrow\widehat{FAM}=90^o\)
Vậy tam giác AFM vuông.
c) Gọi giao điểm của AM và DE là G.
Do FA // DE mà AM vuông góc FA nên AM vuông góc DE.
Vậy thì ta có ngay AFDE là hình chữ nhật.
Suy ra KG giao AD tại trung điểm mỗi đường hay I cũng là trung điểm KG.
Vậy thì AM, DE và KI đồng quy tại điểm G.

Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>góc AED=góc AHD=góc ABC
góc AED+góc MAC=90 độ
=>góc MAC+góc B=90 độ
=>góc MAC=góc C
=>90 độ-góc MAC=90 độ-góc C
=>góc MAB=góc MBA
Xét ΔMAC có góc MAC=góc C
nên ΔMAC cân tại M
=>MA=MC(1)
Xét ΔMAB có góc MAB=góc B
nên ΔMAB cân tại M
=>MA=MB(2)
Từ(1) và(2) suy raMB=MC
hay M là trung điểm của BC
Điểm N ở đâu vậy bạn?