KY
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
22 tháng 4 2018
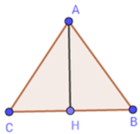
Cạnh của tam giác đều là: AB = BC = CA = 18 : 3 = 6(cm)
Gọi AH là đường cao kẻ từ đỉnh A của tam giác ABC
Khi đó AH vừa là đường cao vừa là đường trung tuyến của tam giác đều ABC.
Suy ra BH = HC = BC = 1 2 .6 = 3(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AHB ta có:
AH = A B 2 − B H 2 = 6 2 − 3 2 = 27 = 3 3 (cm)
Diện tích tam giác đều là:
SABC = A H . B C 2 = 3 3 .6 2 = 9 3 (cm2)
Đáp án cần chọn là: C
22 tháng 8 2020
Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~
TN
1
7 tháng 1 2016
giả sử cạnh của tam giác đều là a
ta áp dụng pitago ta tính được đường cao là \(\sqrt{a^2-\frac{1}{2}a^2}=\frac{\sqrt{3}}{2}a\)
Diện tích của tam giác là \(S=\frac{1}{2}.a.\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{4}a^2\)
theo bài ra : \(S=\frac{\sqrt{3}}{4}a^2=121\sqrt{3}\)
\(\Rightarrow a^2=484\Rightarrow a=22\)
vậy chu vi tam giác đều là C= 22.3 = 66cm
CM
7 tháng 5 2018
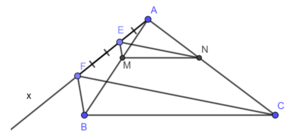
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Gọi p' và S' là chu vi và diện tích của △ AMN.
Trong △ ABC, ta có: MN // BC
Suy ra: △ AMN đồng dạng ΔABC
PN
1
DN
6 tháng 1 2017
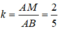
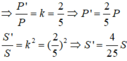
CÓ chu vi = 30 =) AB = AC = BC = 30 : 3 = 10 = ) diỆn tích = 10 x 10 x 10 =1000
D
23 tháng 1 2022
a. Ta có: ▲ABC∼▲MNP (gt)
=>\(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{AH}{MQ}=k=\dfrac{1}{3}\) (với AH,MQ lần lượt là đường cao của tam giác ABC, MNP)
\(\dfrac{S_{ABC}}{S_{MNP}}=k^2=\dfrac{1}{9}\)
b. Ta có: \(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{1}{3}\)(cmt)=>PMNP=3PABC
*PMNP-PABC=60cm
=>3PABC-PABC=60cm
=>2PABC=60cm
=>PABC=30cm ; PMNP=90cm
c. Ta có: \(\dfrac{S_{ABC}}{S_{MNP}}=\dfrac{1}{9}\)(cmt)=>SMNP=9SABC
*SMNP+SABC=640cm2
=>9SABC+SABC=640cm2
=>10SABC=640cm2
=>SABC=64cm2 ; SMNP=576cm2
2 tháng 6 2015
a) Tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng 2/3
=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=\frac{2}{3}\)=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=\frac{AB+BC+AC}{DE+EF+DF}=\frac{2}{3}\)
=> \(\frac{C_{ABC}}{C_{DEF}}=\frac{2}{3}\) (Kí hiệu \(C\) là chu vi) => \(C_{DEF}=\frac{3}{2}.C_{ABC}=\frac{3}{2}.8=12\) cm
b)
+) Dễ có tam giác DEK đồng dạng với tam giác ABH (do góc DEK = ABH; góc DKE = AHB)
=> \(\frac{AB}{DE}=\frac{AH}{DK}\) Mà \(\frac{AB}{DE}=\frac{2}{3}\Rightarrow\frac{AH}{DK}=\frac{2}{3}\)
+) Có : \(\frac{S_{ABC}}{S_{DEF}}=\frac{\frac{1}{2}.AH.BC}{\frac{1}{2}.DK.EF}=\frac{AH}{DK}.\frac{BC}{EF}=\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\)
=> \(S_{ABC}=\frac{4}{9}.S_{DEF}=\frac{4}{9}.27=12\) cm2
*) Tổng quát: Nếu tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng k
=> \(\frac{C_{ABC}}{C_{DEF}}=k;\frac{S_{ABC}}{S_{DEF}}=k^2\)