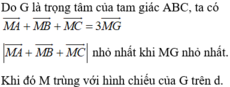Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là trọng tâm tam giác
\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(=\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là chân đường vuông góc hạ từ G xuống BC hay M là trung điểm BC
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=3MG=AM=\dfrac{a\sqrt{3}}{2}\)

Ủa biểu thức là \(\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\) hay \(\left|\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\right|\) em? Vì vecto không có khái niệm min max, chỉ độ dài vecto mới có min, max thôi
dạ, có dấu giá trị tuyệt đối ạ, do em không gõ ra cái dấu đó được nên bị thiếu ạ.

Gọi G là trọng tâm tam giác ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\)
\(P=\left(\overrightarrow{MA}\right)^2+\left(\overrightarrow{MB}\right)^2+\left(\overrightarrow{MC}\right)^2\)
\(=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3MG^2+GA^2+GB^2+GC^2\)
Mà \(GA^2+GB^2+GC^2\) cố định \(\Rightarrow P_{min}\) khi \(MG_{min}\)
\(\Rightarrow MG\perp BC\) \(\Rightarrow M\) là trung điểm BC