Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: D và E đối xứng nhau qua AB
nên AD=AE(1)
Ta có: D và F đối xứng nhau qua AC
nên AD=AF(2)
Từ (1) và (2) suy ra AE=AF
b: Khi E đối xứng với F qua A thì A là trung điểm của EF
Xét ΔEDF có
DA là đườg trung tuyến
DA=EF/2
Do đó: ΔEDF vuông tại E
=>\(\widehat{BAC}=90^0\)

Gọi I,K lần lượt là giao điểm của AB với DE, AC với DF
a) E đối xứng D qua AB \(\Rightarrow\) IE = ID; góc I = 90 độ
Xét tam giác AED có AI là đường trung tuyến (IE = ID) còn là đường cao (góc I = 90 độ)
nên tam giác AED cân tại A \(\Rightarrow\) AE = AD (1)
F đối xứng D qua AC \(\Rightarrow\) KF = KD; góc K = 90 độ
Xét tam giác AFD có AK là đường trung tuyến (KF = KD) còn là đường cao (góc K = 90 độ)
nên tam giác AFD cân tại A \(\Rightarrow\) AF = AD (2)
Từ (1) và (2) \(\Rightarrow\) AE = AF
b) không biết làm

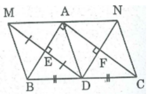
Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 1/2 AB; AF = 1/2 AC
Nên AE = AF ⇒ AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

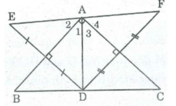
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
⇒ ∠ A 3 = ∠ A 4
∠ (EAF) = ∠ EAD) + ∠ (DAF) = ∠ A 1 + ∠ A 2 + ∠ A 3 + ∠ A 4 = 2( ∠ A 1 + ∠ A 3 ) = 2 . 90 0 = 180 0
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.