Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ∆ADB và ∆ ACD có:
\(\widehat{B}\) =\(\widehat{C}\)(gt) (1)
\(\widehat{A1}\)=\(\widehat{A2}\)(AD là tia phân giác)
Nên \(\widehat{D1}\)=\(\widehat{D2}\)
AD cạnh chung.
Do đó ∆ADB=∆ADC(g.c.g)
b) ∆ADB=∆ADC(câu a)
Suy ra AB=AC .
a Xét \(\Delta ADB\) và \(\Delta ADC\) có :
AD : cạnh chung
\(\widehat{BAD}=\widehat{CAD}\) (gt)
Ta có : \(\widehat{BDA}+\widehat{DAB}+\widehat{ABD}=\widehat{CDA}+\widehat{DAC}+\widehat{ACD}\)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}\)
\(\Rightarrow\Delta ADB=\Delta ADC\) (g . c . g)
b Vì \(\Delta ADB=\Delta ADC\)
\(\Rightarrow\) AB = AC
![]()

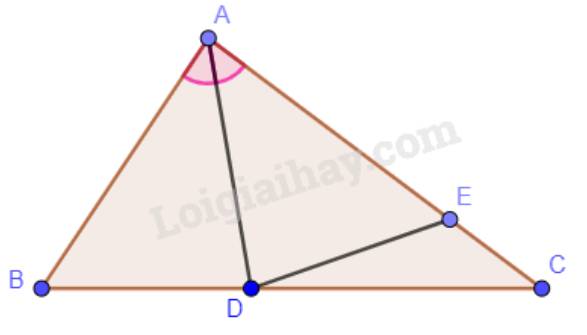
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).

MK K BIẾT VIẾT KÍ HIỆU GÓC NÊN CÓ GÌ TỰ HIỂU NHÉ.
a. xét 2 tam giác abd và tam giác ADC, ta có :
B = C (gt)
A1=A2(gt)
=> góc còn lại của 2 tam giác này cũng phải bằng nhau
=> ADB = ADC( tự nhìn hình)
Xét tam giác ADB và tam giác ADC, ta có:
A1 = A2(gt)
AD : canh chung
D1 = D2 ( cmt)
=> Tam giác ADB = tam giác ADC (g.c.g)(đpcm)
b.=> AB = AC ( 2 cạnh tương ứng của 2 tam giác bằng nhau)(đpcm)
bài này thầy giáo giảng cho mk rồi. tk mk nhé bạn. cảm ơn!! ^.^

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

Hướng dẫn bạn làm nhé, bài này cũng đơn giản thôi :P
a/ \(\Delta ABD=\Delta ACD\left(c.g.c\right)\)
b/ \(\Delta AHD=\Delta AKD\left(canhhuyen...gocnhon\right)\)
\(\Rightarrow HD=KD\)
c/ tự làm

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
b: Sửa đề: DM\(\perp\)AB tại M. Chứng minh AC\(\perp\)DN
Xét ΔAMD và ΔAND có
AM=AN
\(\widehat{MAD}=\widehat{NAD}\)
AD chung
Do đó: ΔAMD=ΔAND
=>\(\widehat{AMD}=\widehat{AND}\)
mà \(\widehat{AMD}=90^0\)
nên \(\widehat{AND}=90^0\)
=>DN\(\perp\)AC
c: Xét ΔKCD và ΔKNE có
KC=KN
\(\widehat{CKD}=\widehat{NKE}\)(hai góc đối đỉnh)
KD=KE
Do đó: ΔKCD=ΔKNE
d: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Ta có: ΔKCD=ΔKNE
=>\(\widehat{KCD}=\widehat{KNE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NE//DC
=>NE//BC
ta có: NE//BC
MN//BC
NE,MN có điểm chung là N
Do đó: M,N,E thẳng hàng
Xin lỗi các bạn nhưng mk bt câu trả lời rồi! Lỡ đăng
a/ \(\Delta ADB\) có : \(\widehat{D_1}=180^0-\left(\widehat{A_1}+\widehat{B}\right)\)(1) ( tổng 3 góc trong 1 tam giác )
\(\Delta ADC\) có : \(\widehat{D_2}=180^0-\left(\widehat{A_2}+\widehat{C}\right)\) (2) ( tổng 3 góc .... )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{D_1}=\widehat{D_2}\)
Xét \(\Delta ADB\) và \(\Delta ADC\) có:
\(\widehat{A_1}=\widehat{A_2}\) ( tia phân giác góc A )
\(AD\) cạnh chung
\(\widehat{D_1}=\widehat{D_2}\left(cmt\right)\)
Do đó \(\Delta ADB=\Delta ADC\left(g.c.g\right)\)
b/ Vì \(\Delta ADB=\Delta ADC\left(cmt\right)\Rightarrow AB=AC\) ( cạnh tương ứng )
Hình như ở câu a bạn phai thêm điều kiện là:
góc B = góc C theo gt
góc A1 = góc A2 vì A là tia phân giác
nhưng nếu làm theo cách của bạn thì phait thêm Đk trên thì phải