K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

10 tháng 3 2018
P/s hình tự vẽ lấy :)
Ta có: AM cắt CK tại E
Xét tam giác AMB và tam giác EMC có:
\(MB=MC\left(gt\right)\)
\(\widehat{AMB}=\widehat{CME}\)( đối đỉnh )
\(\widehat{ABM}=\widehat{ECM}\)( so le trong và AB // CE )
\(\Rightarrow\Delta AMB=\Delta EMC\left(g-c-g\right)\)
\(\Rightarrow MA=ME\)( hai cạnh tương ứng )
Và BM = MC ( Vì M là trung tuyến AM )
Suy ra ABCE là hình bình hành
\(\Rightarrow BE//AC\Rightarrow\frac{IB}{ID}=\frac{IA}{IE}\left(1\right)\)
\(\Rightarrow\frac{IB}{IK}=\frac{IA}{IE}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\frac{ID}{IB}=\frac{IB}{IK}\)
\(\Rightarrow IB^2=ID.IK\left(đpcm\right)\)
Vậy \(IB^2=ID.IK\)

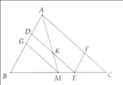
Xét tam giác ABC có BD và AM là 2 đường trung tuyến cắt nhau tại I
=> I là trọng tâm tam giác ABC
=> \(\frac{IB}{ID}=\frac{2}{1}\)(1)
Vì AK//BC nên \(\frac{IK}{IB}=\frac{IA}{IM}=\frac{2}{1}\)
=> \(\frac{KB}{IB}=\frac{IB}{IB}+\frac{IK}{IB}=1+\frac{2}{1}=\frac{3}{1}\)
\(\frac{KD}{IB}=\frac{IK}{IB}-\frac{ID}{IB}=\frac{2}{1}-\frac{1}{2}=\frac{3}{2}\)
\(\Rightarrow\frac{KB}{KD}=\frac{3}{1}:\frac{3}{2}=\frac{2}{1}\)(2)
Từ (1) , (2) => Đpcm