Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đối xứng của A qua trục tung là A'(4; -1) và đối xứng của A qua trục hoành là A"(-4; 1).
Vậy đỉnh thứ hai của tam giác cân là I(-4; -1).
Ta có thể tính được hệ số góc của đường thẳng AI bằng công thức:
\(m=\dfrac{y_A-y_I}{x_A-x_I}=\dfrac{1-\left(-1\right)}{4-\left(-4\right)}=\dfrac{1}{4}\)
Vậy phương trình đường thẳng AI là:
\(y-y_A=m\left(x-x_A\right)\)
\(y-1=\dfrac{1}{4}\left(x-4\right)\)
\(4y-4=x-4\)
\(x-4y=0\)
Vậy phương trình đường thẳng cần tìm là \(x-4y=0\)
Đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ sẽ qua điểm trung điểm của đoạn thẳng BC, ký hiệu là M.
Có:
Tọa độ x của trung điểm M = \(\dfrac{x_B+x_C}{2}=\dfrac{3+1}{2}=2\)
Tọa độ y của trung điểm M = \(\dfrac{y_B+y_C}{2}=\dfrac{2+6}{2}=4\)
Vậy tọa độ của điểm M là (2, 4).
Phương trình đường thẳng đi qua A và M là:
\(y-1=\dfrac{4-1}{2-4}.\left(x-4\right)\Rightarrow y=-1,5x+7\)y
Vậy phương trình đường thẳng cần tìm là \(y=-1,5x+7.\)
(Cái câu kia mình làm cho bài khác tính cop màn hình mà bấm gửi nhầm ở đây, bài giải này mới đúng nhé!)

Phương trình đường thẳng qua điểm C là: 5x + 3y - 21 = 0
Tìm điểm D trên đường thẳng BC sao cho AD là đường cao của tam giác ABC.
Diện tích tam giác ABD là: \(S_{ABD} = \dfrac{1}{2} \cdot 1 \cdot \dfrac{2}{3} = \dfrac{1}{3}\)
Diện tích phần chứa điểm B là: \(S_{BCD} = \dfrac{1}{3}\)
Diện tích phần chứa điểm A là: \(S_{ACD} = S_{ABC} - S_{ABD} - S_{BCD} = \dfrac{1}{2} \cdot 1 \cdot \sqrt{26} - \dfrac{1}{3} - \dfrac{1}{3} = \dfrac{1}{2} \cdot \sqrt{26} - \dfrac{2}{3}\)
Vậy ta cần tìm điểm D sao cho AD là đường cao của tam giác ABC và \(S_{ACD} = 2S_{BCD}\)
Giải hệ phương trình tìm được D(2;4).
Vậy phương trình đường thẳng chia tam giác thành hai phần, phần chứa điểm A có diện tích gấp đôi phần chứa điểm B là: 5x - 3y - 7 = 0.

a: \(\overrightarrow{AB}=\left(-11;11\right);\overrightarrow{AC}=\left(-2;6\right)\)
Vì -11/-2<>11/6
nên A,B,C thẳng hàng
ABCD là hình bình hành
=>vecto DC=vecto AB
=>5-x=-11 và 4-y=11
=>x=16 và y=-7
b: \(\overrightarrow{BH}=\left(x+4;y-9\right)\); vecto BC=(9;-5); vecto AH=(x-7;y+2)
Theo đề, ta có:
(x+4)/9=(y-9)/-5 và 9(x-7)+(-5)(y+2)=0
=>-5x-20=9y-81 và 9x-63-5y-10=0
=>-5x-9y=-61 và 9x-5y=73
=>x=481/53; y=92/53
c: Vì (d') vuông góc (d) nên (d'): 4x+3y+c=0
Thay x=-2 và y=3 vào (d'), ta được:
c+4*(-2)+3*3=0
=>c=-1

Giả sử A(a;0), B(0;b)
Vì tam giác OAB có trọng tâm G(1;3) nên:
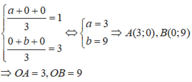
Phương trình AB có dạng:
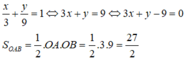

goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
