Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔABC có BE,CF là các đường cao
BE cắt CF tại H
=>H là trực tâm
=>AH vuông góc BC
Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hình bình hành
2: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>M là trung điểm của HD
Xét ΔDAH có
M,O lần lượt là trung điểm của DH,DA
nên MO là đường trung bình
=>AH=2MO

Mình giải câu a nha ( bạn nào biết làm câu b với câu c thì giúp bạn ấy )
a) Gọi AD ; BE ; CF là đường cao của t/g ABC
=> CE vuông góc với AB
BE vuông góc với AC
Mà Bx vuông góc với AB
=> Bx // CE
Cy vuông góc với AC
=> Cy // BE
=> tứ giác BHCD là hình bình hành

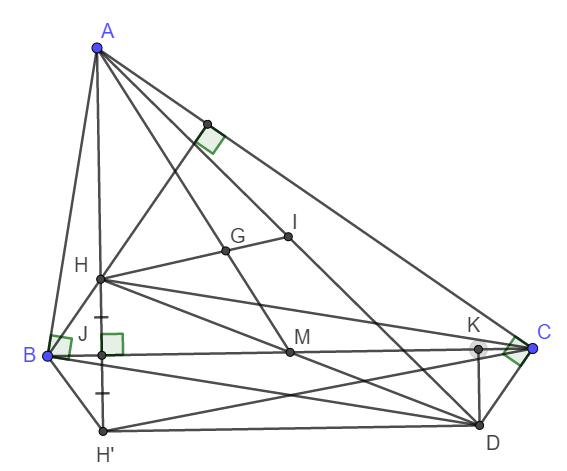
a) Ta thấy H là trực tâm tam giác ABC nên CH vuông góc AB. Suy ra DB song song CH.
Tương tự BH song song DC (Cùng vuông góc AC)
Vậy nên tứ giác BHCD là hình bình hành.
Do BHCD là hình bình hành nên \(\Delta BHC=\Delta CDB\left(c-g-c\right)\)
Lại có H' đối xứng với H qua BC nên \(\Delta BHC=\Delta BH'C\left(c-c-c\right)\)
Vậy thì \(\Delta CDB=\Delta BH'C\)
Gọi J là giao điểm của HH' và BC. Kẻ DK vuông góc BC tại K.
Khi đó ta có ngay H'J = KD. Vậy nên JKDH' là hình bình hành hay JK//H'D
Suy ra tứ giác BCDH' là hình thang.
Lại có : H'C = BD (Cùng bằng HC) nên BCDH' là hình thang cân.
b) Do BHCD là hình bình hành nên giao điểm của HD và BC là trung điểm mỗi đường. Ta gọi điểm đó là M.
Xét tam giác AHD có AM là trung tuyến, \(AG=\frac{2}{3}AM\) nên G là trọng tâm tam giác.
Vậy thì HG đi qua trung điểm AD, hay H, G, I thẳng hàng.
d) Để hình bình hành BHCD là hình thoi thì BH = HC. Vậy thì AH là đường cao đồng thời trung trực nên tam giác ABC là tam giác cân tại A.
Để hình bình hành BHCD là hình chữ nhật thì HC vuông góc BH. Lại có HC//BD nên BD//BH. Vậy thì BH trùng AB. Tương tự CH trùng AC.
Suy ra để BHCD là hình chữ nhật thì tam giác ABC vuông tại A.

a: Xét tứ giác BHCD có
BH//CD
CH//BD
DO đó: BHCD là hình bình hành
Câu b và c sai đề rồi bạn

a: Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HD