Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

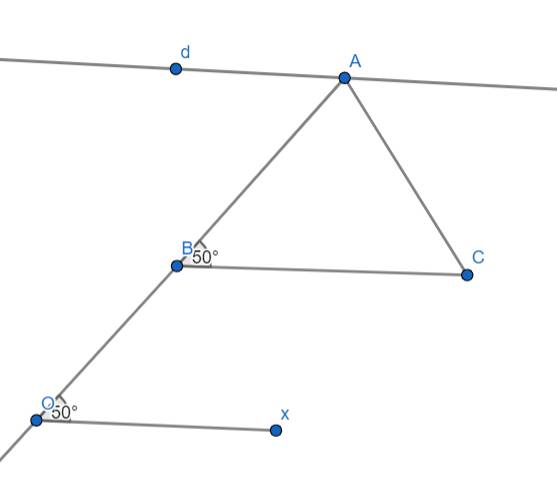
a) Ta có:
\(\widehat{xOB}=50^o\left(gt\right)\)
\(\widehat{CBA}=50^o\left(gt\right)\)
\(\Rightarrow\widehat{xOB}=\widehat{CBA}\)
Mà hai góc này ở vị trí đồng vị nên:
\(\Rightarrow Ox//BC\)
b) Ta có:
\(d//BC\left(gt\right)\)
Và: \(BC//Ox\left(cmt\right)\)
\(\Rightarrow d//Ox\)

Giả sử n^2 + 2006 = m^2 (m,n la số nguyên)
Suy ra n^2 - m^2 =2006 <==> ( n - m )( n + m ) = 2006
Gọi a = n - m, b = n + m ( a,b cũng là số nguyên)
Vì tích của a và b bằng 2006 la một số chẵn, suy ra trong 2 số a và b phải có ít nhất 1 số chẵn (1)
Mặt khác ta có: a + b = (n - m) + (n + m) = 2n là 1 số chẵn ==> a và b phải cùng chẵn hoặc cùng lẻ(2)
Từ (1) và (2) suy ra a và b đều là số chẵn
Suy ra a = 2k , b= 2l ( với k,l là số nguyên)
Theo như trên ta có a.b = 2006 hay 2k.2l = 2006 hay 4.k.l = 2006
Vì k,l là số nguyên nên suy ra 2006 phải chia hết cho 4 ( điều này vô lý, vì 2006 không chia hết cho 4)
Vậy không tồn tại số nguyên n thỏa mãn đề bài đã cho.(đpcm)
Giả sử n^2 + 2006 = m^2 (m,n la số nguyên)
Suy ra n^2 - m^2 =2006 <==> ( n - m )( n + m ) = 2006
Gọi a = n - m, b = n + m ( a,b cũng là số nguyên)
Vì tích của a và b bằng 2006 la một số chẵn, suy ra trong 2 số a và b phải có ít nhất 1 số chẵn (1)
Mặt khác ta có: a + b = (n - m) + (n + m) = 2n là 1 số chẵn ==> a và b phải cùng chẵn hoặc cùng lẻ(2)
Từ (1) và (2) suy ra a và b đều là số chẵn
Suy ra a = 2k , b= 2l ( với k,l là số nguyên)
Theo như trên ta có a.b = 2006 hay 2k.2l = 2006 hay 4.k.l = 2006
Vì k,l là số nguyên nên suy ra 2006 phải chia hết cho 4 ( điều này vô lý, vì 2006 không chia hết cho 4)
Vậy không tồn tại số nguyên n thỏa mãn đề bài đã cho.(đpcm)
k cho mk nha
HT

Bạn tự vẽ hình nha![]()
a.
- BOx = 500
- ABC = 500
=> BOx = ABC
mà 2 góc này ở vị trí so le trong
=> Ox // BC
BAC + CAO = 1800
800 + CAO = 1800
CAO = 1800 - 800
CAO = 1000
Ay là tia phân giác của CAO
=> OAy = yAC = \(\frac{CAO}{2}\) = \(\frac{100^0}{2}\) = 500
mà ABC = 500
=> OAy = ABC
mà 2 góc này ở vị trí đồng vị
=> Ay // BC.
b.
- d _I_ BC
- Ox // BC
=> d _I_ Ox.
Chúc bạn học tốt![]()