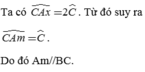Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác abc có góc b bằng góc c . Gọi am là tia phân giác của góc ngoài đỉnh a. Chứng tỏ am//bc

Bạn kham khảo link này nhé.
Câu hỏi của Nguyễn Minh Hường - Toán lớp 7 - Học toán với OnlineMath

Tam giác ABC có: góc B +góc C + góc BAC = 180o => 40o + 40o + BAC = 180o => góc BAC = 180o - 80o = 100o
=> góc BAy = 180o - BAC = 180o - 100o = 80o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80o/2 = 40o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40o) Mà hai góc này ở vị trí SLT => Ax // BC

ta có góc BAC+B+C=180 độ=> BAC=180-50-50=80 độ
ta có góc IAB=180 độ-BAC=180-80=100 độ (IAB là góc ngoài ở đỉnh A)
mà Am la pg=> IAm=mAB=IAB:2=100:2=50 độ
ta có góc IAm= góc C=50 độ ,2 góc này ở vị trí đồng vị
=> Am// BC
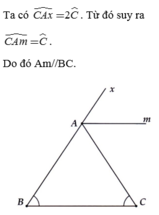
ta có hình vẽ:
Theo tính chất góc ngoài của tam giác , ta có: góc CAn = góc B +góc C= 50+50=100 độ
=> góc CAm= góc CAn : 2= 100 độ :2 = 50 độ
=> Am // BC ( so le trong)

Tam giác ABC có: góc B +góc C + góc BAC = 180 o => 40 o + 40 o + BAC = 180 o => góc BAC = 180 o - 80 o = 100 o
=> góc BAy = 180 o - BAC = 180 o - 100 o = 80 o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80 o/2 = 40 o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40 o) Mà hai góc này ở vị trí SLT => Ax // BC