Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

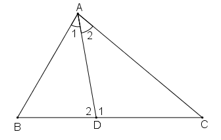
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o

Xét △ABC có: A + B + C = 180o
=> A + 70o + 40o = 180o
=> A = 70o
Vì AD là phân giác của A
=> BAD = DAC = A/2 = 70o / 2 = 35o
Xét △ABC có: DAC + C + ADC = 180o
=> 35o + 40o + ADC = 180o
=> ADC = 105o
Ta có: ADC + ADB = 180o (2 góc kề bù)
=> 105o + ADB = 180o
=> ADB = 75o

Ta có góc B - góc C = 30 độ
(góc B + góc A1) - (góc C + góc A2) = 30 độ
góc D2 - góc D1 = 30 độ
mà D1 + D2 = 180 độ (kề bù)
⇔ góc D1 = (180 độ - 30 độ) : 2 = 75 độ
góc D2 = 180 độ - 75 độ = 105 độ
Vậy góc ADB = 75 độ; ADC = 105 độ

Đặt \(\widehat{ADC}=b;\widehat{ADB}=a\)
Ta có: \(a+\widehat{B}+\widehat{BAD}=b+\widehat{C}+\widehat{CAD}\)
\(\Leftrightarrow a+\widehat{C}+20^0=b+\widehat{C}\)
\(\Leftrightarrow a-b=-20\)
mà a+b=180
nên 2a=160
=>a=80
=>b=100