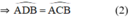Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Học sinh tự chứng minh
b, Học sinh tự chứng minh
c, Học sinh tự chứng minh
d, Chú ý: B I A ^ = B M A ^ , B M C ^ = B K C ^
=> Tứ giác BICK nội tiếp đường tròn (T), mà (T) cũng là đường tròn ngoại tiếp DBIK. Trong (T), dây BC không đổi mà đường kính của (T) ≥ BC nên đường kính nhỏ nhất bằng BC
Dấu "=" xảy ra <=> B I C ^ = 90 0 => I ≡ A => MA
a: góc MDC=1/2*sđ cung MC=90 độ
=>góc BDC=90 độ
Xét tứ giác ABCD có
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
b: ABCD nội tiếp
=>góc BCA=góc BDA
=>góc BCA=góc SCA
=>CA là phân giác của góc SCB
c: Gọi N là giao của MH với AB
góc MHC=1/2*180=90 độ
=>NH vuông góc BC
Xét ΔCBN có
NH,CA là đường cao
NH cắt CA tại M
=>M là trực tâm
=>BM vuông góc CN
=>C,D,N thẳng hàng
=>MH,CD,BA đồng quy
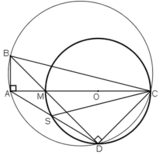
a)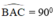 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
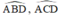đều là góc nội tiếp chắn cung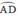 
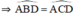
c) + Trong đường tròn đường kính MC:
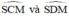đều là các góc nội tiếp cùng chắn cung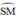 
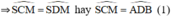
+ Trong đường tròn đường kính BC:
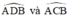đều là các góc nội tiếp chắn cung 
