Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ ΔADE có ∠E1 là góc ngoài ⇒ ∠E1 > ∠A
Mà ∠A > 90o ⇒ ∠E1 > 90o
ΔCDE có ∠E1 tù ⇒ CD là cạnh lớn nhất ⇒ CD > DE (1)
+ Tương tự xét ΔADC có ∠D1 là góc ngoài
⇒ ∠D1 > ∠A ⇒ ∠D1 > 90o (vì ∠A > 90º)
ΔBDC có ∠D1 tù ⇒ BC là cạnh lớn nhất ⇒ BC > CD (2)
Từ (1) và (2) suy ra BC > DE.

a) Xét tam gics BAD và BED ta có:
BD là cạnh chung (gt)
AB=AE (gt)
Góc ABD=góc DBC ( vid BD là phân giác của gốc B)
=> Tam giác BAD=tam gics BED (c.g.c)
=>AD=DE ( 2 cạnh tương ứng)
=> Tam giác BAD= tam giác BED
=> góc BAD=BED(2 góc tương ứng)
=>BED=BAD=90*
Xét tam giác ABC và EDC ta cosL'
BAC=DEC=90*
góc C chung
=> tam giác ABC~tam giác EDC (g-g)
=> goác ABC=EDC
b) Xét tam giác ABE ta có:
AB=BE
=> tam giác ABE cân tại B
mà BD là tia phân giác của góc B
=> BD là đường cao
=> BD vuông góc vs AE

*Tự vẽ hình
a) Xét tam giác ABD và EBD có :
\(\widehat{ABD}=\widehat{DBE}\left(gt\right)\)
BD : cạnh chung
BA=BE(gt)
=> Tam giác ABD=EBD(c.g.c)
=> AD=DE
và \(\widehat{BAD}=\widehat{DEB}=90^o\)
\(\Rightarrow\widehat{BAD}=\widehat{DEC}=90^o\)
b) Gọi giao điểm của BD và AE là O
Tam giác ABO=EBO(c.g.c) (tự cm)
=> \(\widehat{BOA}=\widehat{BOE}\)
Mà : \(\widehat{BOA}+\widehat{BOE}=180^o\)
\(\Rightarrow\widehat{BOA}=90^o\)
\(\Rightarrow AE\perp BD\left(đccm\right)\)
#H

Xét \(\Delta CDE\) có \(\widehat{E_1}>\widehat{A}\), mà \(\widehat{A}\) là góc tù nên \(\widehat{E_1}\) là góc tù.
Suy ra CD > DE. (1)
Xét \(\Delta BCD\) có \(\widehat{D_1}>\widehat{A}\) nên \(\widehat{D_1}\) là góc tù. Suy ra BC > CD. (2)
Từ (1) và (2) suy ra BC > DE.
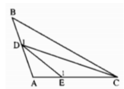
a ) Ta có : gócA = 90o
=> gócD1 và gócB1 đều là góc nhọn ( vì trong tam giác vuông thì có một góc vuông và 2 góc nhọn )
=> gócD1 < 90o ( Số đo của góc nhọn luôn luôn bé hơn số đo của góc vuông )
=> gócD1 < gócA ( 1 )
Mà : gócD1 là góc đối diện của BA
( 2 )
: gócA là góc đối diện của BD
Từ ( 1 ) và ( 2 ) suy ra : BA < BD ( Vì trong một tam giác cạnh đối diện với góc lớn hơn thì có số đo lớn hơn ) ( 3 )
Ta có : gócD1 + gócD2 = gócADC ( DB nằm giữa DA và DC )
=> gócD2 = gócADC - gócD1 = góc bẹt - góc nhọn = góc tù ( Vì góc bẹt = 180o , góc nhọn bé hơn 90o )
=> gócD2 > 90o ( Vì số đo của góc tù lớn hơn góc vuông )
=> gócD2 > gócA ( 4 )
Mà : gócA là góc đối diện với BD
( 5 )
: gócD2 là góc đối diện với BC
Từ ( 4 ) và ( 5 ) suy ra : BC > BD ( Vì trong tam giác cạnh đối diện với góc có số đo lớn hơn thì lớn hơn ) ( 6 )
Từ ( 3 ) và ( 6 ) suy ra : BA < BD < BC ( điều phải chứng minh )
b ) Ta có : gócD2 > gócA ( cmt ) ( 7 )
Mà : gócD2 là góc đối diện với BC
( 8 )
: gócA là góc đối diện với DE
Từ ( 7 ) và ( 8 ) suy ra : BC > DE ( Vì trong tam giác cạnh đối diện với ............................................ )
Học tốt !
Góc A > 90 độ mà bn