Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác abe va acf
co ;goc f=goc e =90
goc a chung
2 tam giuac dong dang
a) Xét ΔABE và ΔACE có:
\(\widehat{AEB}=\widehat{AFC}\) \(=90^0\)
\(\widehat{CAB}:chung\)
=> ΔABE∼ΔACE (g.g)
b) Xét ΔFHB và ΔEHC có:
\(\widehat{HFB}=\widehat{HEC}\) \(=90^0\)
\(\widehat{FHB}=\widehat{EHC}\) (2 góc đối đỉnh)
=> ΔFHB∼ΔEHC (g.g)
=> \(\frac{HF}{HE}=\frac{HB}{HC}\Leftrightarrow HF.HC=HB.HE\) (đpcm)
c) Theo câu a) ta có: ΔABE∼ΔACF
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét ΔBAC và ΔEAF có:
\(\widehat{BAC}:chung\)
\(\frac{AB}{AC}=\frac{AE}{AF}\) (cmtrn)
=> ΔBAC∼ΔEAF (c.g.c)
=> \(\widehat{AEF}=\widehat{ABC}\) (2 góc tương ứng)

hình tự vẽ:
a)Vì BE là tpg của ^ABC(gt)
=>^ABE=^EBH(=^EBC)
Xét tam giác ABE vuông ở A và tam giác HBE vuông ở H có:
BE:cạnh chung
^ABE=^EBH(cmt)
=>tam giác ABE=tam giác HBE(ch-gn)
b)Vì tam giác ABE=tam giác HBE(cmt)
=>AB=HB(cặp cạnh t.ư)
Xét tam giác ABH có:AB=HB(cmt)
=>tam giác ABH cân ở B(DHNB0
Xét tam giác ABH cân ở B có:AE là tpg của ^ABH(vì AE là tpg của ^ABC)
=>BE là đg trung trực của AH (t/c tam giác cân)
c)Vì tam giác ABE=tam giác HBE(cmt)
=>AE=HE(cặp cạnh t.ư)
Ta có:EC>EH (trong tam giác vuông,cạnh huyền là cạnh lớn nhất)
Mà AE=HE(cmt)
=>EC>AE

Đáp án D
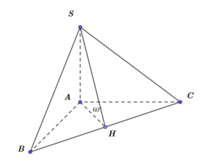
Góc giữa cạnh SA và đáy là SAF ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
A F = 3 2 a ; S F = 3 2 a
Vậy tan S A F ^ = 1 ⇒ S A G ^ = 45 0

b/ Chứng tỏ EDFH là hbh :
Ta có: EH vuông với BF , DF vuông với BF => EH // DF (1)
FH vuông với BE , DE vuông với BE => FH // DE (2)
Từ (1) + (2) => EDFH là hbh








giải giúp với .........