Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có: \(\dfrac{AB}{AD}=\dfrac{AM}{AI}=\dfrac{1}{2}\)
⇒ DI // BM
mà M ∈ BC ⇒ DI // BC ( 1 )
b) Ta có: \(\dfrac{BA}{AD}=\dfrac{CA}{CE}=\dfrac{1}{2}\)
⇒ BC // DE ( 2 )
Từ ( 1) và ( 2) có: DE // BC (cmt) và DI // BC (cmt)
Ta thấy qua điểm D nằm ngoài BC kẻ được 2 đường thẳng song song với BC, điều này trái với tiên đề Ơ-clít nên hai đường thẳng DE và DI phải trùng nhau
⇒ D, I, E cùng nằm trên một đường thẳng
⇒ D, I, E thẳng hàng
1) Xét ΔADI có
B là trung điểm của AD(gt)
M là trung điểm của AI(gt)
Do đó: BM là đường trung bình của ΔADI(Định nghĩa đường trung bình của tam giác)
Suy ra: BM//DI(Định lí 2 về đường trung bình của tam giác)
hay DI//BC
a) Ta có: \(\frac{AB}{AD}=\frac{AC}{AE}=\frac{1}{2}\) → BC//DE
→ \(\frac{BC}{DE}=\frac{1}{2}\Rightarrow DE=2\cdot BC=14=18\left(cm\right)\)
AD = 2AB = 10 (cm); AE = 2AC = 14 (cm)
b) Ta có: \(\frac{AB}{AD}=\frac{AM}{AI}=\frac{1}{2}\) → DI//BM
mà M thuộc BC → DI//BC
c) Ta có: DE//BC (cmt) và DI//BC (cmt)
ta thấy qua điểm D nằm ngoài BC kẻ được 2 đường thẳng song song với BC, điều này trái với tiên đề Ơ-clít nên hai đường thẳng DE và DI phải trùng nhau
→ D, I, E cùng nằm trên một đường thẳng
→ D, I, E thẳng hàng
a) Ta có : \(\frac{AB}{AD}=\frac{AC}{AD}=\frac{1}{2}\rightarrow BC\)//DE
\(\frac{\rightarrow BC}{DE}=\frac{1}{2}=>DE=2.BC=14=18\left(cm\right)\\ \)
\(AD=2AB=10\left(cm\right)AE=2AC=14\left(cm\right)\)
b) Ta có : \(\frac{AB}{AD}=\frac{AM}{AI}=\frac{1}{2}\rightarrow DI\)//BM
mà M thuộc BC ->DI//BC
c) Ta có : \(DE\)//BC(cmt) và DI//BC(cmt)
ta thấy qua điểm D nằm ngoài BC kẻ được 2 đường thẳng song song với BC , điều này trái với tiêu đề Ơ-clit nên hai đường thẳng DE và DI phải trùng nhau
->D.I.E cùng nằm trên một đường thẳng
->D.I.E thẳng hàng
a: AB=BD
nên B là trung điểm của AD
=>AD=2AB=10(cm)
AC=CE
nên C là trung điểm của AE
=>AE=2AC
=>AE=14(cm)
Xét ΔADE có
B là trung điểm của AD
C là trung điểm của AE
Do đó: BC là đường trung bình
=>BC//DE
Xét ΔADE có BC//DE
nên BC/DE=AB/AD=1/2
=>9/DE=1/2
=>DE=18(cm)
b: Xét ΔADI có
B là trung điểm của AD
M là trung điểm của AI
Do đó: BM là đường trung bình
=>BM//DI
hay DI//BC
c: Ta có: DI//BC
DE//BC
mà DI cắt DE tại D
nên D,I,E thẳng hàng
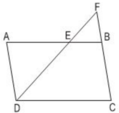
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA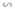 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB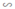 
ΔDEA
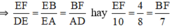
⇒ EF = 5cm, BF = 3,5cm.
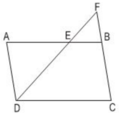
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB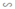 
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB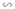 
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA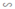 
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB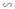 
ΔDEA
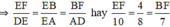
⇒ EF = 5cm, BF = 3,5cm.
a: Xét ΔHAD vuông tại H và ΔBCD vuông tại B có
\(\widehat{HDA}=\widehat{BDC}\)
Do đó; ΔHAD~ΔBCD
b: ta có; ΔHAD~ΔBCD
=>\(\widehat{BCD}=\widehat{HAD}\)
mà \(\widehat{BCD}=\widehat{ACD}\)
nên \(\widehat{HAD}=\widehat{ACD}\)
Xét ΔHAD vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAD}=\widehat{HCA}\)
Do đó: ΔHAD~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HD}{HA}\)
=>\(HA^2=HD\cdot HC\)
c: Ta có: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=10^2-6^2=64\)
=>\(BC=\sqrt{64}=8\left(cm\right)\)
Xét ΔCBA có CD là phân giác
nên \(\dfrac{BD}{BC}=\dfrac{DA}{CA}\)
=>\(\dfrac{BD}{8}=\dfrac{DA}{10}\)
=>\(\dfrac{BD}{4}=\dfrac{DA}{5}\)
mà BD+DA=BA=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{DA}{5}=\dfrac{BD+DA}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
=>\(DA=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)