Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề ra, ta có:\(S_{ABC}=180cm^2\)
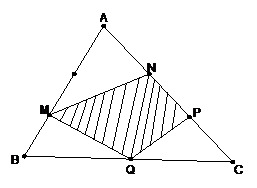
\(\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{AM}{AB}\times\dfrac{AN}{AC}=\dfrac{2}{3}\times\dfrac{1}{3}=\dfrac{2}{9}\)
\(\dfrac{S_{BMQ}}{S_{ABC}}=\dfrac{BM}{BA}\times\dfrac{BQ}{BC}=\dfrac{1}{3}\times\dfrac{1}{2}=\dfrac{1}{6}\)
\(\dfrac{S_{CPQ}}{S_{ABC}}=\dfrac{CP}{CA}\times\dfrac{CQ}{CB}=\dfrac{1}{3}\times\dfrac{1}{2}=\dfrac{1}{6}\)
\(\Rightarrow S_{MNPQ}=S_{ABC}-S_{AMN}-S_{BMQ}-S_{CPQ}=1-\dfrac{2}{9}-\dfrac{1}{6}-\dfrac{1}{6}=\dfrac{4}{9}S_{ABC}=\dfrac{4}{9}\times180=80cm^2\)


Nối N với B
Xét hai tam giác ABN và ABC :
- Chung chiều cao hạ từ đỉnh B xuống cạnh AC
- AN = 1/3 AC
=> SABN = 1/3 x SABC = 180 x 1/3 = 60 ( cm2)
Xét hai tam giác AMN và ABC :
- Chung chiều cao hạ từ đỉnh N xuống cạnh AB
- AM = 2/3 AB
=> SAMN = 2/3 x SABN = 60 x 2/3 = 40 ( cm2)
Nối M với C
Xét hai tam giác BMC và ABC :
- Chung chiều cao hạ từ đỉnh C xuống cạnh AB
- BM = 1/3 AB
=> SBMC = 1/3 x SABC = 180 x 1/3 = 60 ( cm2)
Xét hai tam giác BMQ và BMC :
- Chung chiều cao hạ từ đỉnh M xuống cạnh BC
- BQ = 1/2 BC
=> SBMQ = 1/2 x SBMC = 60 x 1/2 = 30 ( cm2)
Nối P với B
Xét hai tam giác PBC và ABC :
- Chung chiều cao hạ từ đỉnh B xuống cạnh AC
- PC = 1/3 AC
=> SPBC = 1/3 x SABC = 180 x 1/3 = 60 ( cm2)
Xét hai tam giác PQC và PBC :
- Chung chiều cao hạ từ đỉnh P xuống cạnh BC
- QC = 1/2 BC
=> SPQC = 1/2 x SPBC = 60 x 1/2 = 30 ( cm2)
Vậy diện tích hình MNPQ là :
180 - 40 - 30 - 30 = 80 ( cm2)
Đáp số : 80 cm2

Em kham khảo link này nhé.
Câu hỏi của Cô Nàng Cá Tính - Toán lớp 6 - Học toán với OnlineMath
Chắc chắn có 100%

Cho mình xin cái hình vẽ mình sẽ giải hộ cho bạn
Chúc bạn có kì nghỉ hè vui vẻ

Nối n với b, a với q
Diện tích ABQ là
180 :2 = 90
Diện tích MBQ là
90:3 = 30
Diện tích PQC là
90:3=30
Diện tích ABN là
180 :3 = 60
Diện tích AMN là
60:3x2=40
Diện tích MNPQ là
180 -(30 + 30 + 40 )= 80

a) Xét tam giác ABC và ABQ có: chung chiều cao hạ từ A xuống BC; đáy BC = 2 lần đáy BQ
=> S(ABC) = 2 x S(ABQ)
b) +) Xét tam giác ABQ và BMQ có: chung chiều cao hạ từ Q xuống AB; đáy AB = 3 lần đáy BM
=> S(ABQ) = 3 x S(BMQ)
Mà S(ABC) = 2 x S(ABQ) = 2 x 3 x (MBQ) = 6 x S(MBQ)
Vậy ....
c) S(BMQ) = S(ABC)/6 = 180/6 = 30 cm2
+) Tương tự ý a; b ta có: S(AQC) = S(ABC)/2 và S(PQC) = S(AQC)/3
=> S(PQC) = S(ABC)/6 = 180/6 = 30 cm2
+) Nối với M với C:
S(AMC) = 2/3 x S(ABC) ( Vì chung chiều cao hạ từ C xuống AB; đáy AM = 2/3 đáy AB)
Và S(AMN) = 1/3 x S(AMC) (Vì chung chiều cao hạ từ M xuông AC; đáy AN = 1/3 đáy AC)
=> S(AMN) = (1/3) x (2/3) x S(ABC) = 2/9 x S(ABC) = 2/9 x 180 = 40 cm2
Vậy S(BMNQ) = S(ABC) - S(AMN) - S(BMQ) - S(QNC) = 180 - 40 - 30 - 30 = 80 cm2