Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm G cách trung điểm M của BC (cố định) một khoảng cố định bằng .
Kết luận: quỹ tích trọng tâm G của tam giác ABC là đường tròn trừ các giao điểm của đường tròn với BC (do G không thể thuộc BC).

Cần tìm điểm cố định sao cho C cách điểm đó một khoảng cố định.
Dựng điểm D đối xứng với B qua A, khi đó D là điểm cố định, AM là đường trung bình của tam giác BCD, CD = 2AM = 2m (cố định)
Kết luận: Quỹ tích điểm C là đường tròn (D ; 2m), trừ các giao điểm của nó với đường thẳng AB (khi đó tam giác ABC trở thành đoạn thẳng)

1: góc ADC=góc AEC=90 độ
=>ADEC nội tiếp
2: góc ABH=90 độ-góc BAC=góc DEA

d) Gọi I là trung điểm BC,AI cắt EF tại K.H là hình chiếu vuông góc của K trên BC. Chứng minh: AH luôn đi qua một điểm cố định

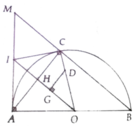
a, HS tự chứng minh
b, Ta có: I A C ^ = I C A ^ => I M C ^ = I C M ^ nếu IM = IA = IC
c, Sử dụng hệ thức lượng cho ∆AMB ta dùng Pytago cho tam giác AMB
d, Kẻ GD//AC (D ∈ OC) => D cố định lại có OI ⊥ AC => OG ⊥ DG
=> G thuộc đường tròn đường kính OD cố định
a: AM^2+BN^2
=CM^2+AC^2+BC^2+CN^2
=AB^2+1/4(AC^2+CB^2)
=5/4BA^2 ko đổi
b: Tập hợp trọng tâm G là (C;2/3CK)(với K là trung điểm của AB)