Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc EBM=góc KBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF
=>ME=MF
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
MF=ME
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC

a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (gt)
AM chung
BM = MC (M là trung điểm BC)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)
\(\Rightarrow AM\) là tia phân giác của \(\widehat{BAC}\)
b) Xét hai tam giác vuông \(\Delta AME\) và \(\Delta AMF\) có:
\(\widehat{AEM}=\widehat{AFM}=90^0\)
AM chung
\(\widehat{MAE}=\widehat{MAF}\) (do AM là tia phân giác của \(\widehat{BAC}\))
\(\Rightarrow\Delta AME=\Delta AMF\) (cạnh huyền - góc nhọn)
\(\Rightarrow AE=AF\) (hai cạnh tương ứng)

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó:ΔAEM=ΔAFM
Suy ra:ME=MF
hay ΔMEF cân tại M
c: Ta có: AE=AF
ME=MF
Do đó: AM là đường trung trực của FE
hay AM⊥FE

a, Xét tam giác AMB và tam giác AMC có
AM _ chung
AB = AC
^MAB = ^MAC
Vậy tam giác AMB = tam giác AMC (c.g.c)
b, Xét tam giác AEM và tam giác AFM có
AM _ chung
^MAE = ^MAF
Vậy tam giác AEM = tam giác AFM (ch-gn)
=> AE = AF ( 2 cạnh tương ứng )
=> EM = FM ( 2 cạnh tương ứng )
Xét tam giác MEF có EM = FM
Vậy tam giác MEF cân tại M
c, AE/AB = AF/AC => EF // BC
mà tam giác ABC cân tại A có AM là phân giác
đồng thời là đường cao
=> AM vuông BC
=> AM vuông EF

a: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc A chung
=>ΔAMB=ΔANC
b: AN=căn 10^2-8^2=6cm=AM
c: Xét ΔNAH vuông tại N và ΔMAH vuông tại M có
AH chung
AN=AM
=>ΔNAH=ΔMAH
=>góc NAH=góc MAH
=>H nằm trên tia phân giác của góc BAC

a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔABM=ΔACM
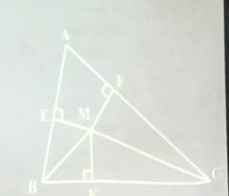
a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc KBM=góc EBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF=ME
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC