Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dùng Pitago đảo thử từng cặp 1 thôi:v
ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)
vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)
\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)

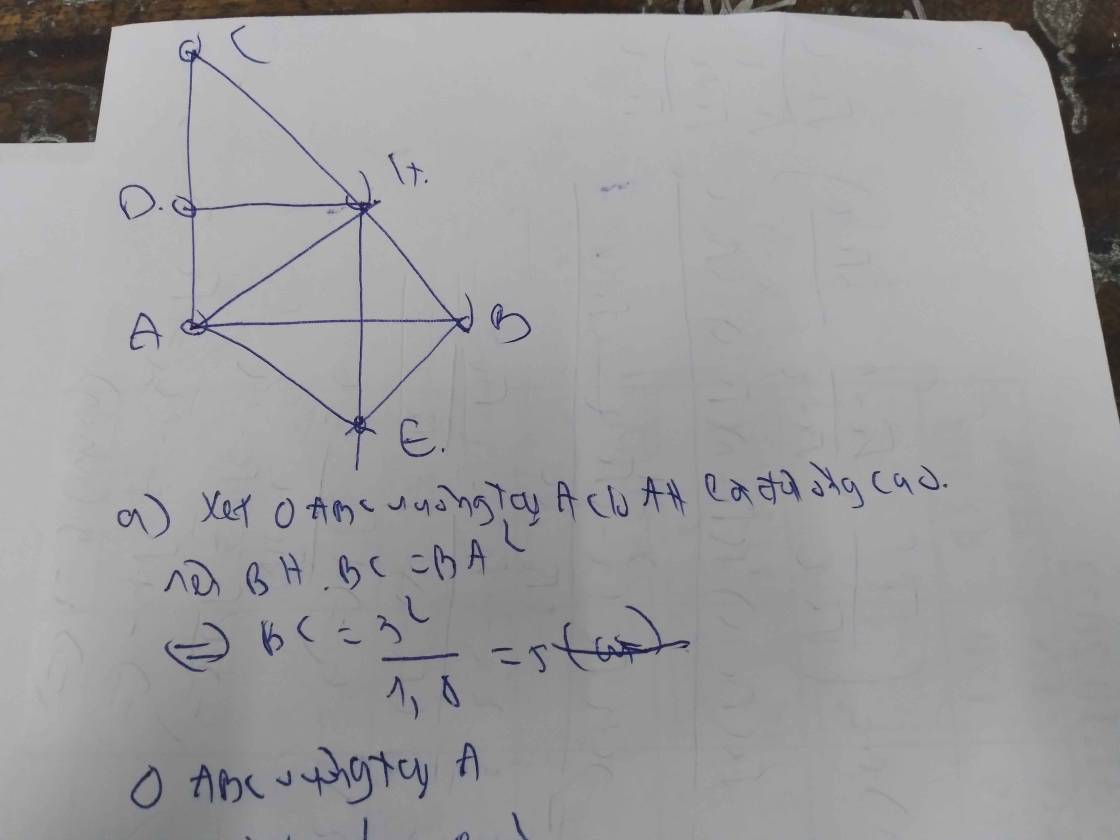
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)

a) Gọi AD là đường kính của ( O ; R )
Có: \(\Delta ADC\) nội tiếp đường tròn ( O ; R ) có O là trung điểm của AD \(\Rightarrow\)\(\Delta ADC\) vuông tại C
Xét 2 tam giác vuông ABH và ADC có: ^ABH = ^ADC ( cùng chắn cung AC ) \(\Rightarrow\)\(\Delta ABH~\Delta ADC\) ( g - g )
\(\Rightarrow\)\(\frac{AB}{AD}=\frac{AH}{AC}\) hay \(\frac{c}{2R}=\frac{h}{b}\)\(\Leftrightarrow\)\(bc=2Rh\)
b) từ a ta có: \(bc=2Rh\)\(\Leftrightarrow\)\(\frac{abc}{4R}=\frac{2Rhc}{4R}=\frac{1}{2}hc=S_{ABC}\) ( đpcm )